Each of equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm; calculate the perimeter and the area of the triangle.

Each of equal sides of an isosceles triangle is 4 cm greater than its height.

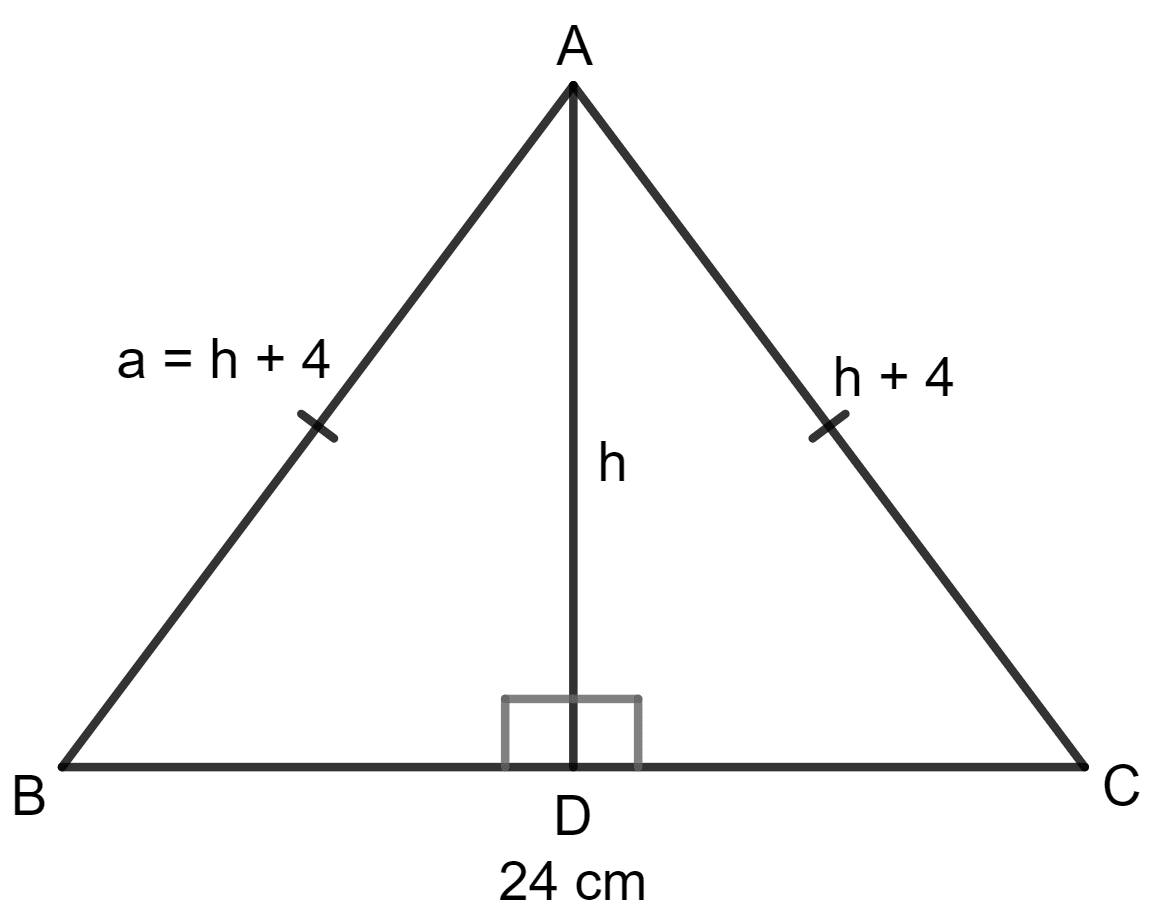
Let h be the height of the triangle.

Equal sides: AB = AC = h + 4

Base: BC = 24 cm

In Δ ABD and Δ ACD,

AD = AD [∵ Common Side]

∠ ADB = ∠ ADC [∵ Both are 90°]

AB = AC [∵ Δ ABC is isosceles]

∴ Δ ABD ≅ Δ ACD [RHS axiom]

∴ BD = CD [C.P.C.T]

∴ BD = CD = $\dfrac{\text{BC}}{2}$ = ${\dfrac{24}{2}}$ = 12 cm

By using the Pythagoras theorem in Δ ABD,

BD² + AD² = AB²

⇒ 12² + h² = (h + 4)²

⇒ 144 + h² = h² + 4² + 2 x h x 4

⇒ 144 + $\cancel{h^2}$= $\cancel{h^2}$+ 16 + 8h

⇒ 144 - 16 = 8h

⇒ 128 = 8h

⇒ h = $\dfrac{128}{8}$

⇒ h = 16 cm

⇒ a = h + 4 = 16 + 4 = 20 cm

Perimeter of triangle = Sum of all sides

= AB + AC + BC

= (20 + 20 + 24) cm

= 64 cm

Area of triangle = $\dfrac{1}{2}$ x base x height

= $\dfrac{1}{2}$ x 24 x 16

= 12 x 16

= 192 cm²

Hence, the perimeter is 64 cm and the area is 192 cm².