Mathematics
The sides of a triangular field are in the ratio 5 : 3 : 4 and its perimeter is 180 m. Find :
(i) its area.
(ii) altitude of the triangle corresponding to its largest side.
(iii) the cost of levelling the field at the rate of ₹ 10 per square metre.
Mensuration
32 Likes
Answer
(i) Given:
The sides of a triangular field are in the ratio 5 : 3 : 4.
Perimeter = 180 m
Let the sides of field be 5a, 3a and 4a.
Perimeter = Sum of all sides of triangular field
⇒ 180 = 5a + 3a + 4a
⇒ 180 = 12a
⇒ a =
⇒ a = 15
Thus, sides of field = 5a , 3a and 4a
= 5 x 15, 3 x 15 and 4 x 15
= 75 m, 45 m and 60 m
Let a = 75 m, b = 45 m and c = 60 m.
∵ Area of triangle =
= m2
= m2
= m2
= 1,350 m2
Hence, the area is 1,350 m2.
(ii) Area = x base x altitude
Base = 75 m
Let h be the altitude of triangle corresponding to the largest side 75 m,
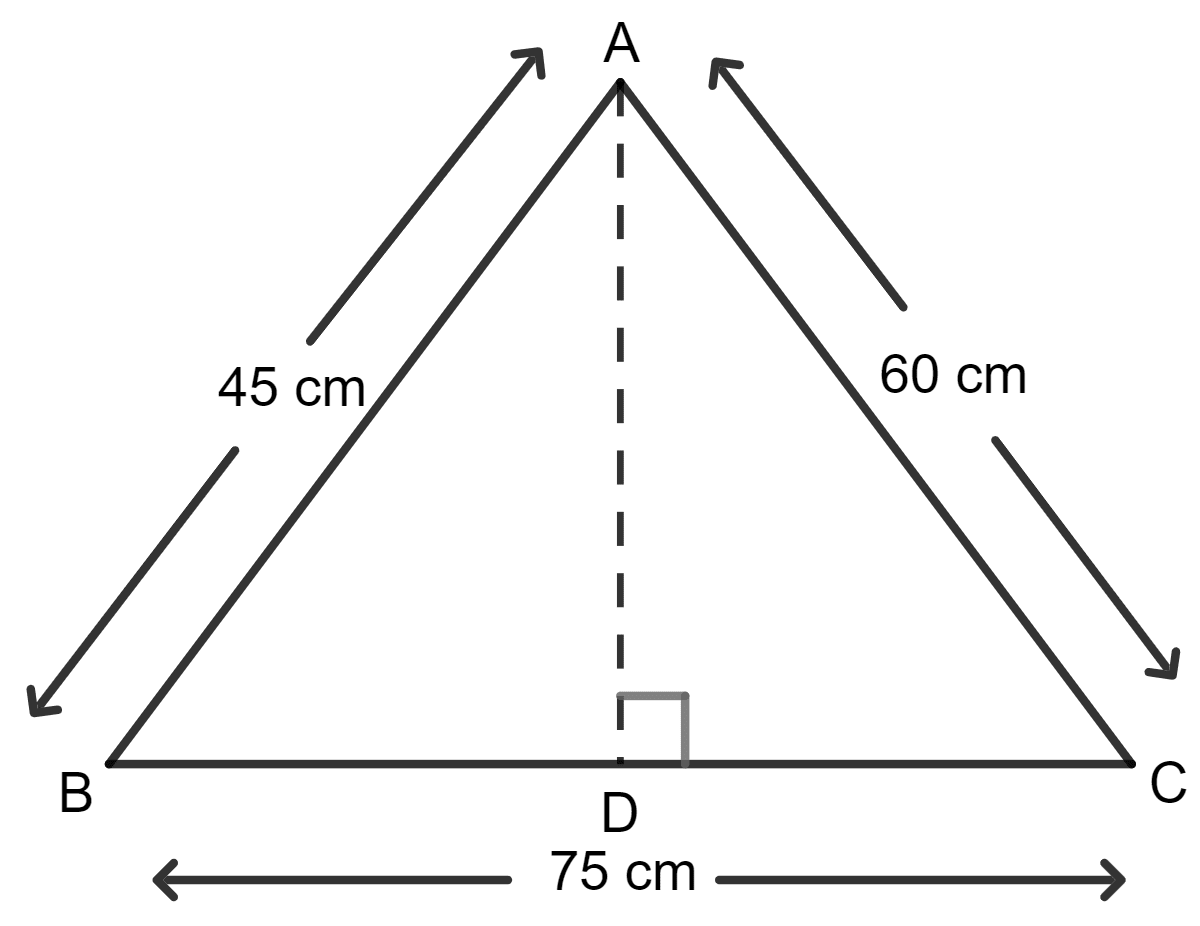
⇒ 1350 = x 75 x h
⇒ h =
⇒ h =
⇒ h = 36 m
Hence, the altitude of the triangle corresponding to its largest side is 36 m.
(iii) Cost of levelling = ₹ 10 per square metre
Total cost = Area x Cost of levelling
= ₹ 1,350 x 10
= ₹ 13,500
Hence, the total cost of levelling is ₹ 13,500.
Answered By
20 Likes
Related Questions
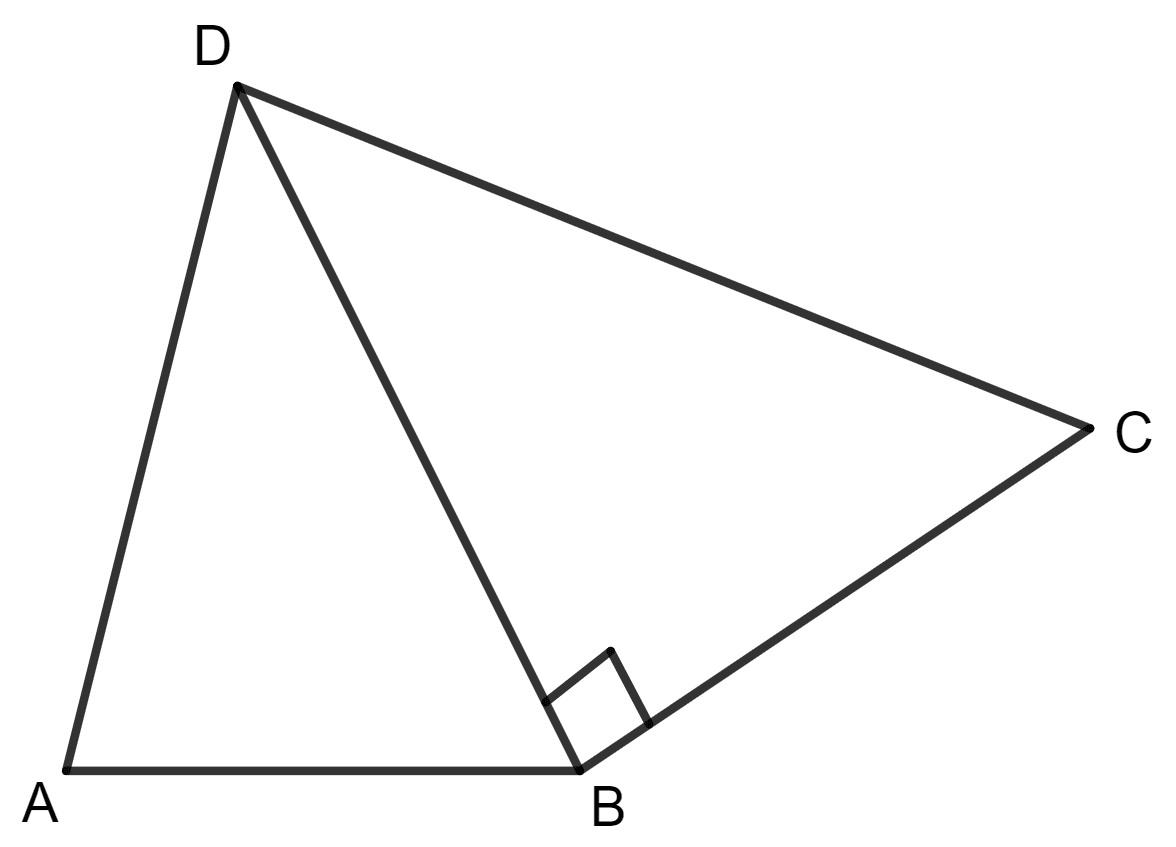
Find the area and the perimeter of quadrilateral ABCD, given below; if, AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
Each of equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm; calculate the perimeter and the area of the triangle.
Calculate the area and the height of an equilateral triangle whose perimeter is 60 cm.