Mathematics
In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that :
(i) M, A and N are collinear.
(ii) A is the mid-point of MN.
Mid-point Theorem
18 Likes
Answer
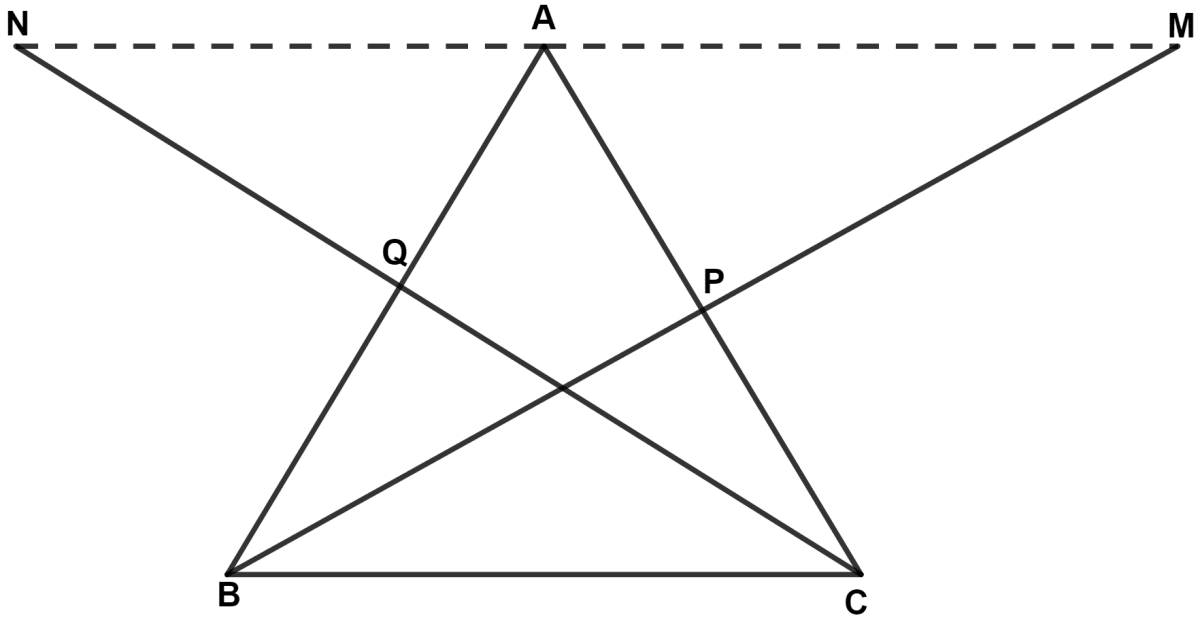
In △ AQN and △ BQC,
⇒ AQ = BQ (Since, CQ is the median)
⇒ QN = CQ (Given)
⇒ ∠AQN = ∠CQB (Vertically opposite angles are equal)
∴ △ AQN ≅ △ BQC (By S.A.S. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ ∠QAN = ∠QBC ……..(1)
⇒ BC = AN ……….(2)
In △ APM and △ CPB,
⇒ AP = CP (Since, BP is the median)
⇒ PM = BP (Given)
⇒ ∠APM = ∠CPB (Vertically opposite angles are equal)
∴ △ APM ≅ △ CPB (By S.A.S. axiom)
⇒ ∠PAM = ∠PCB [By C.P.C.T.C.] ……..(3)
⇒ BC = AM [By C.P.C.T.C.] ……….(4)
(i) In △ ABC,
By angle sum property of triangle,
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ ∠QBC + ∠PCB + ∠BAC = 180°
⇒ ∠QAN + ∠PAM + ∠BAC = 180° [From equations (1) and (3)]
Since, the sum of above angles equal to 180°.
∴ N, A and M lies in a straight line.
Hence, proved that M, A and N are collinear.
(ii) From equations (2) and (4), we get :
⇒ AM = AN.
Hence, proved that A is the mid-point of MN.
Answered By
12 Likes
Related Questions
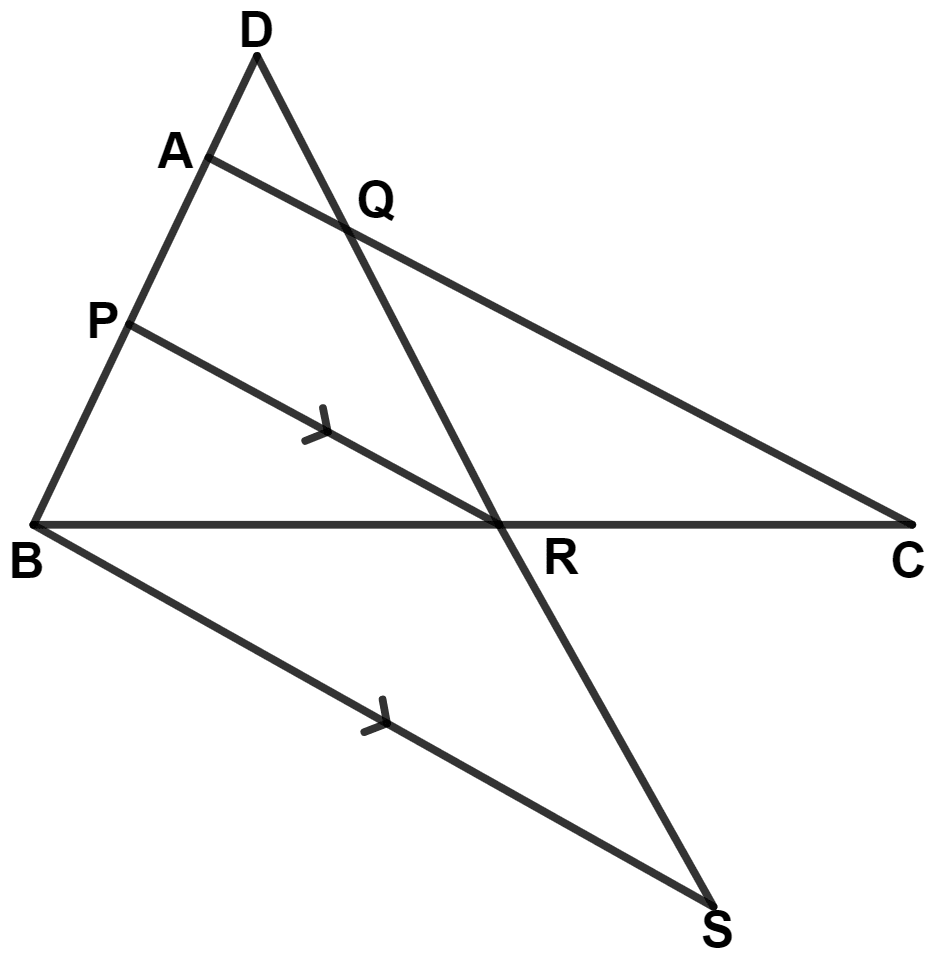
In the figure, given below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that :
(i) AQ // BS
(ii) DS = 3RS
The side AC of a triangle ABC is produced to point E so that CE = . D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that :
(i) 3DF = EF
(ii) 4CR = AB.
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
(i) triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.