Mathematics
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :
(i) triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
Mid-point Theorem
34 Likes
Answer
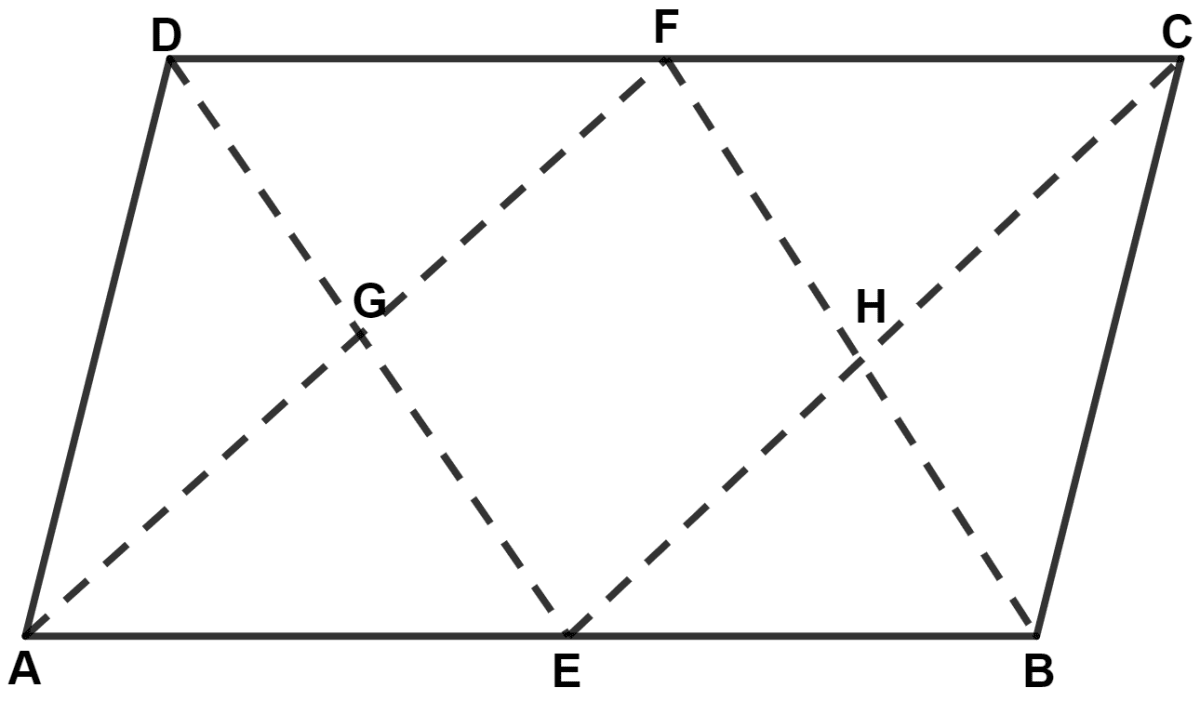
(i) In △ HEB and △ FHC,
⇒ BE = CF (Since, opposite sides of parallelogram are equal i.e. AB = CD and E and F are mid-points of AB and CD respectively)
⇒ ∠HBE = ∠HFC (Alternate angles are equal)
⇒ ∠EHB = ∠FHC (Vertically opposite angles are equal)
∴ △ HEB ≅ △ FHC (By A.A.S. axiom)
Hence, proved that triangles HEB and FHC are congruent.
(ii) Since,
△ HEB ≅ △ FHC
We know that,
Corresponding parts of congruent triangle are equal.
⇒ EH = CH and BH = FH.
⇒ H is the mid-point of BF and CE.
In △ AGE and △ DGF,
⇒ AE = DF (Since, opposite sides of parallelogram are equal i.e. AB = CD and E and F are mid-points of AB and CD respectively)
⇒ ∠GEA = ∠GDF (Alternate angles are equal)
⇒ ∠AGE = ∠DGF (Vertically opposite angles are equal)
∴ △ AGE ≅ △ DGF (By A.A.S. axiom)
∴ AG = GF and EG = DG [By C.P.C.T.C.]
⇒ G is the mid-point of DE and AF.
In △ ECD,
F and H are mid-points of sides CD and EC respectively.
∴ FH || DE [By mid-point theorem]
⇒ FH || GE
F and G are mid-points of sides CD and ED respectively.
∴ GF || EC [By mid-point theorem]
⇒ GF || EH
Since, opposite sides of quadrilateral GEFH are parallel.
Hence, proved that GEHF is a parallelogram.
Answered By
25 Likes
Related Questions
In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that :
(i) M, A and N are collinear.
(ii) A is the mid-point of MN.
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet side BC at points M and N respectively. Prove that :
BM = MN = NC.
In triangle ABC; M is the mid-point of AB, N is mid-point of AC and D is any point in base BC. Use intercept theorem to show that MN bisects AD.