Mathematics
Let angle ABC = 60° and angle ABD = 90°, then ∠CBD is equal to:
150°
30°
150° or 30°
none of these
Quadrilaterals Constructions
1 Like
Answer
From figure (i),
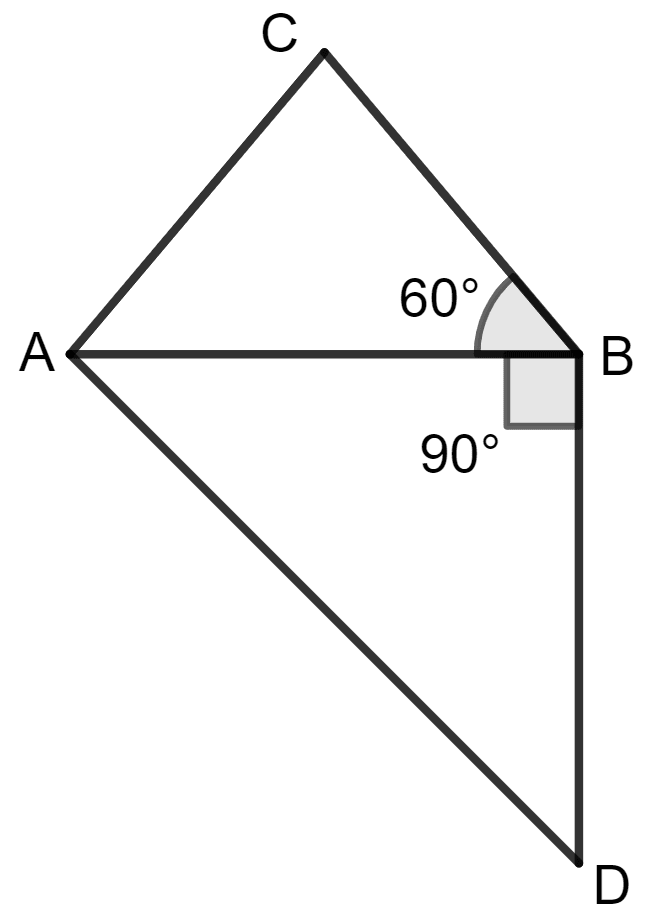
∠ CBD = ∠ ABD + ∠ ABC
= 90° + 60°
= 150°
From figure (ii),
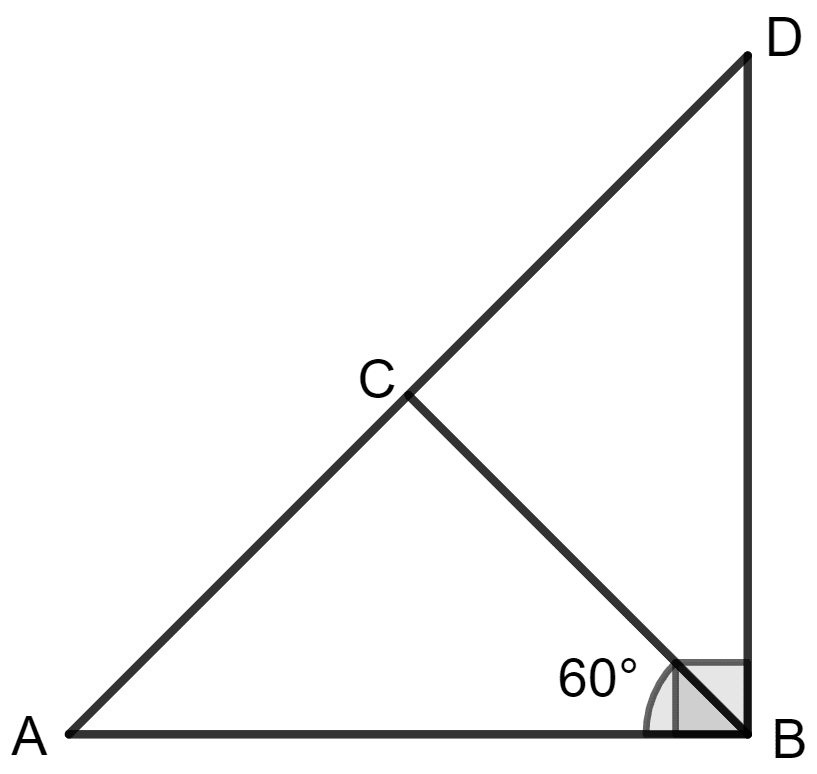
∠ CBD = ∠ ABD - ∠ ABC
= 90° - 60°
= 30°
From figure (iii),
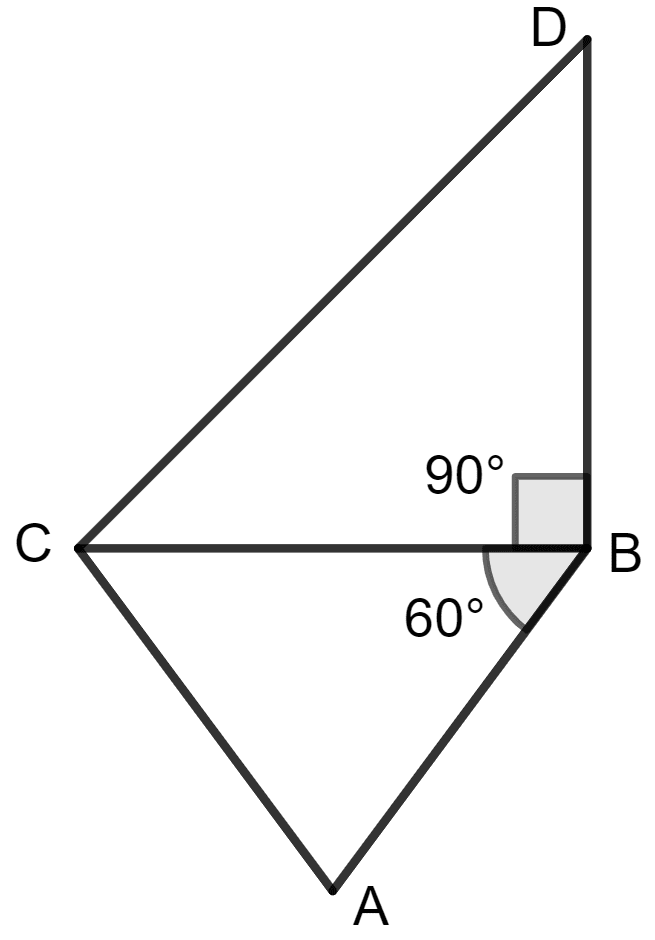
∠ CBD = 90°
Hence, option 4 is the correct option.
Answered By
1 Like
Related Questions
Construct a rhombus ABCD, if:
diagonal AC = 6.6 cm and diagonal BD = 5.8 cm.
Using ruler and compasses only, construct a parallelogram ABCD, in which: AB = 6 cm, AD = 3 cm and ∠DAB = 60°.
In the same figure draw the bisector of angle DAB and let it meet DC at point P. Measure angle APB.
The shortest distance between the point P and the line segment AB is:
PA
PB
line joining point P with the mid-point of AB.
length of perpendicular from point P to line AB.
Two lines AB and CD are not parallel to each other, when they are cut by a transversal with:
vertically opposite angles are equal.
corresponding angles are equal
alternate angles are equal
co-interior angles are supplementary.