KnowledgeBoat Logo
|

Mathematics

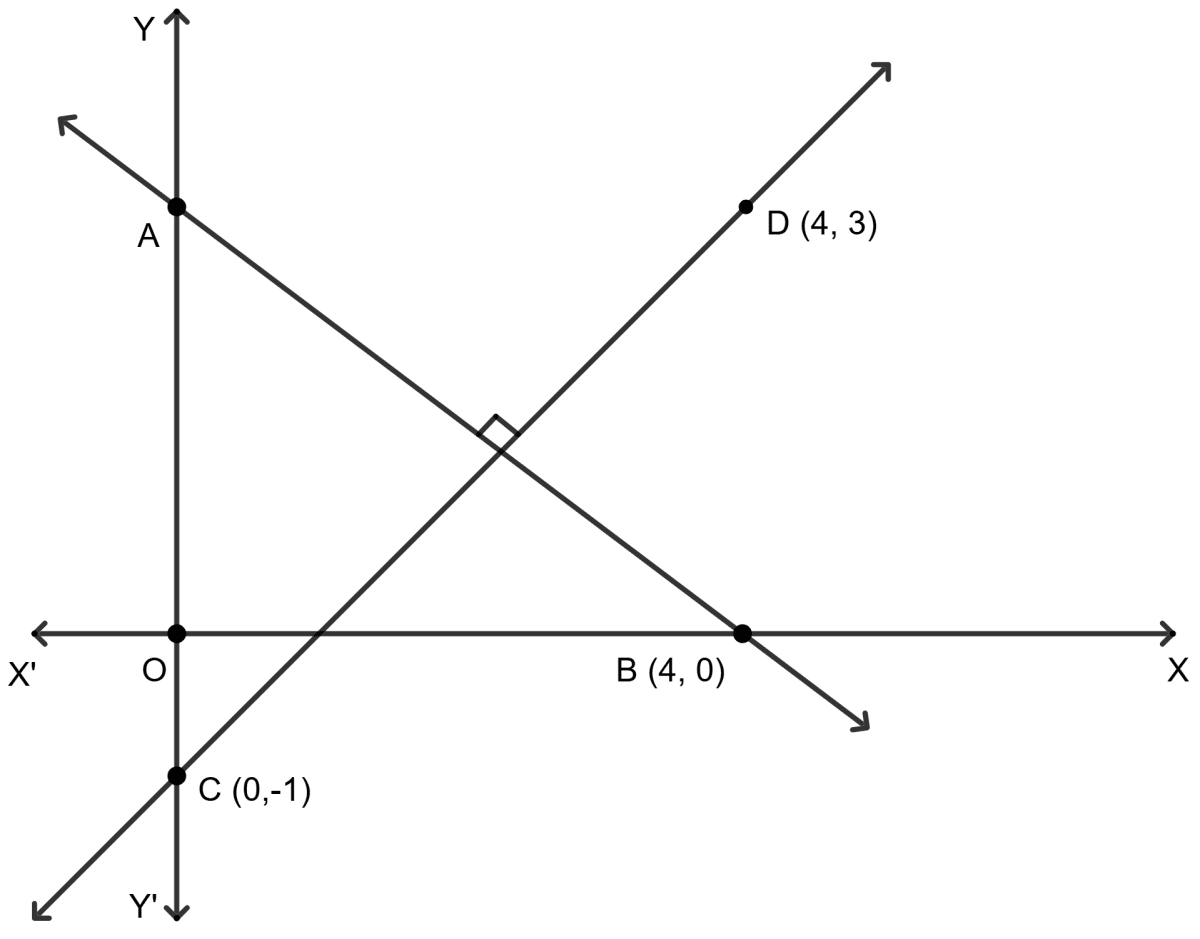
Line AB is perpendicular to line CD. Coordinates of B, C and D are (4, 0), (0, -1) and (4, 3) respectively. Find

(i) the slope of CD

(ii) the equation of line AB

Line AB is perpendicular to line CD. Coordinates of B, C and D are (4, 0), (0, -1) and (4, 3) respectively. Find the slope of CD (ii) the equation of line AB. Equation of a Straight Line, ML Aggarwal Understanding Mathematics Solutions ICSE Class 10.

Straight Line Eq

22 Likes

Answer

(i) By formula,

Slope of a line = y2−y1x2−x1\dfrac{y2 - y1}{x2 - x1}

Substituting values we get :

Slope of CD = 3−(−1)4−0=44\dfrac{3 - (-1)}{4 - 0} = \dfrac{4}{4} = 1.

Hence, slope of CD = 1.

(ii) We know that,

The product of slope of two perpendicular lines equals to -1.

∴ Slope of AB × Slope of CD = -1

⇒ Slope of AB × 1 = -1

⇒ Slope of AB = -1.

By point-slope formula,

Equation of line :

⇒ y - y1 = m(x - x1)

Equation of AB :

⇒ y - 0 = -1(x - 4)

⇒ y = -x + 4

⇒ x + y = 4.

Hence, equation of AB is x + y = 4.

Answered By

10 Likes

Related Questions