Mathematics
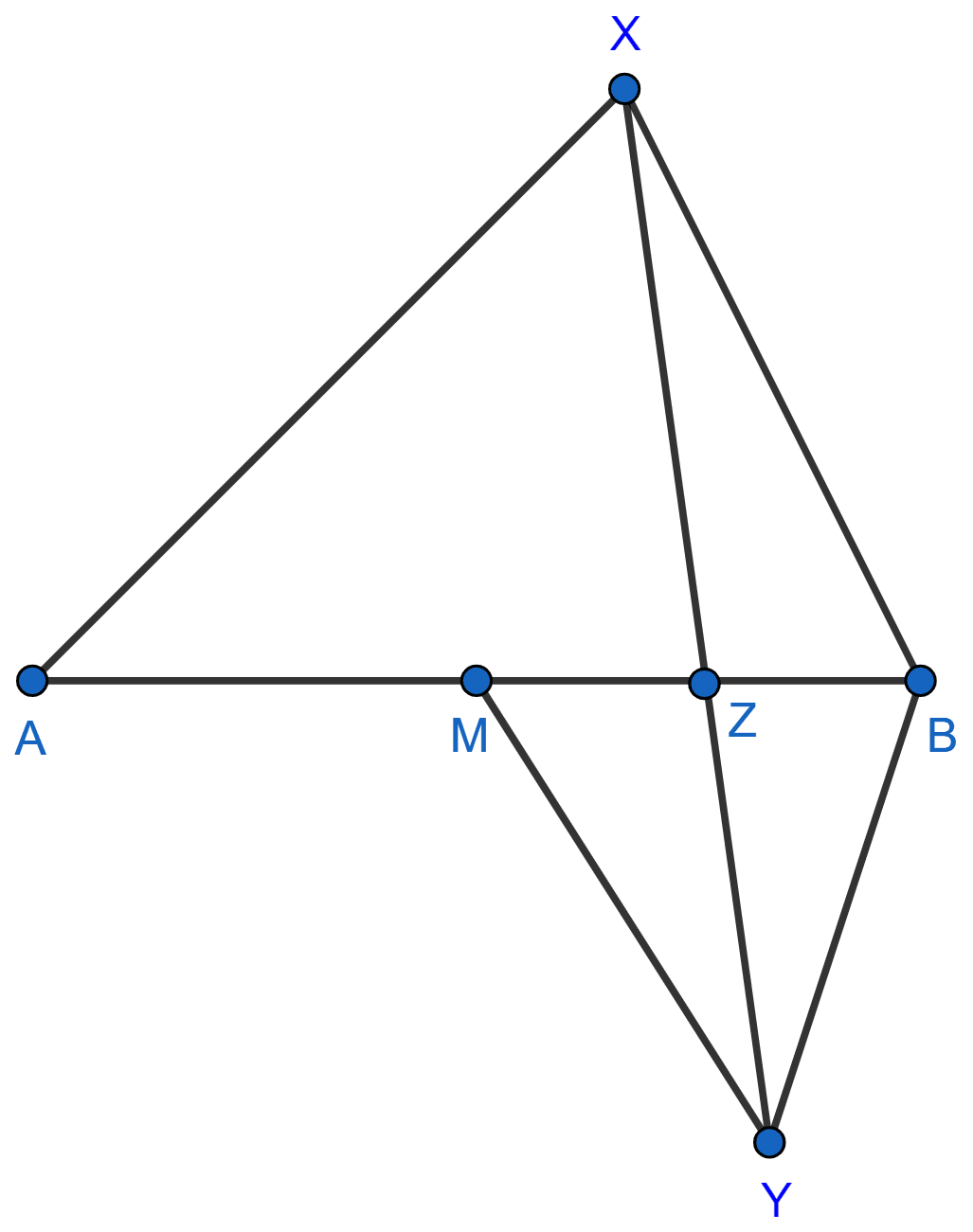
M is the mid-point of a line segment AB; AXB and MYB are equilateral triangles on opposite sides of AB; XY cuts AB at Z. Prove that : AZ = 2ZB.
Similarity
43 Likes
Answer
In △XZB and △MZY,
∠XZB = ∠MZY (Vertically opposite angles are equal)
∠XBZ = ∠YMZ (Each = 60°)
△XZB ~ △MZY [By AA postulate]
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
∴
As sides of equilateral triangle are equal so,
BX = AB
and
MY = MB
∴
∴ ……(1)
As, M is the mid-point of AB.
∴ MB =
From (1),
Hence, proved that AZ = 2ZB.
Answered By
23 Likes
Related Questions
Find :
(i) equation of AB
(ii) equation of CD
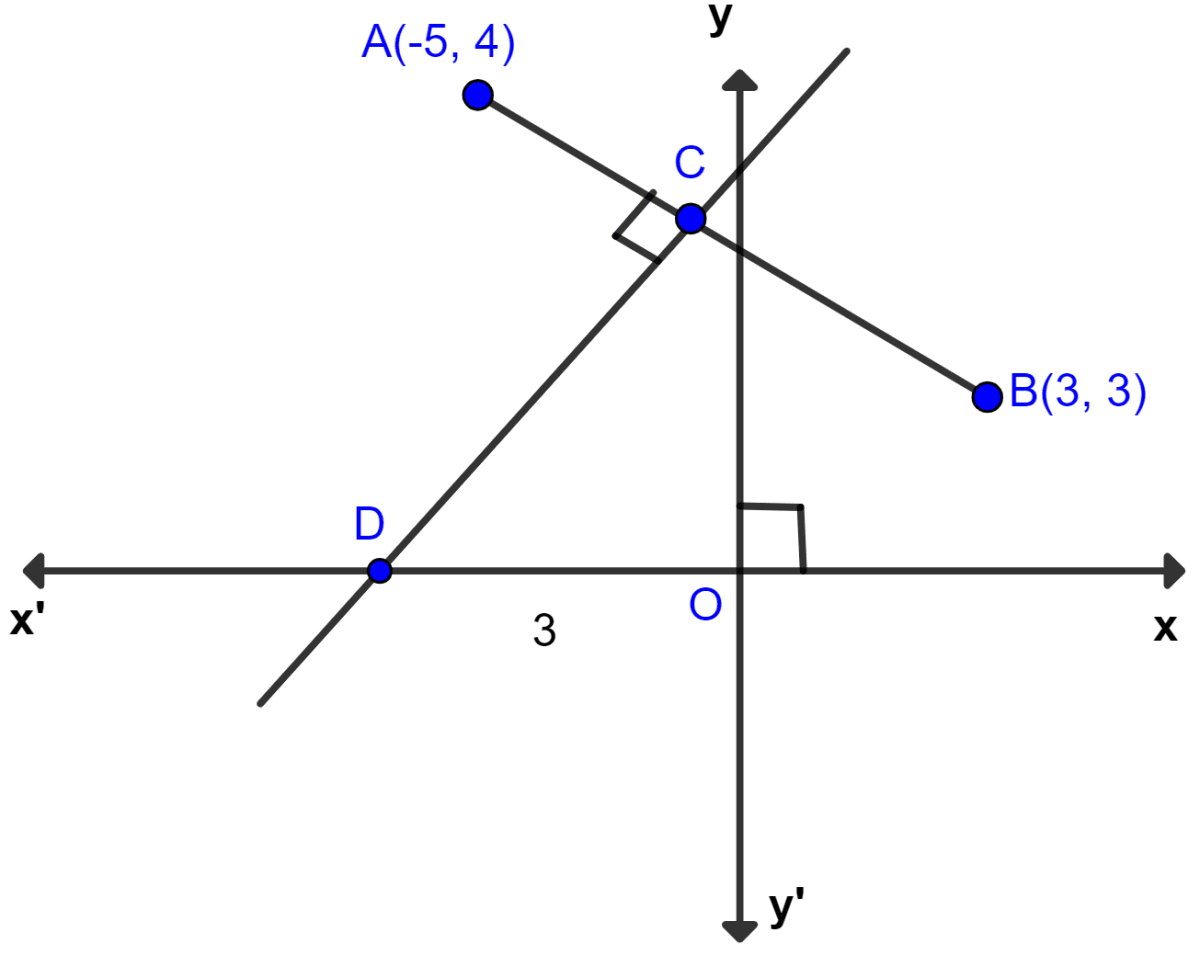
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
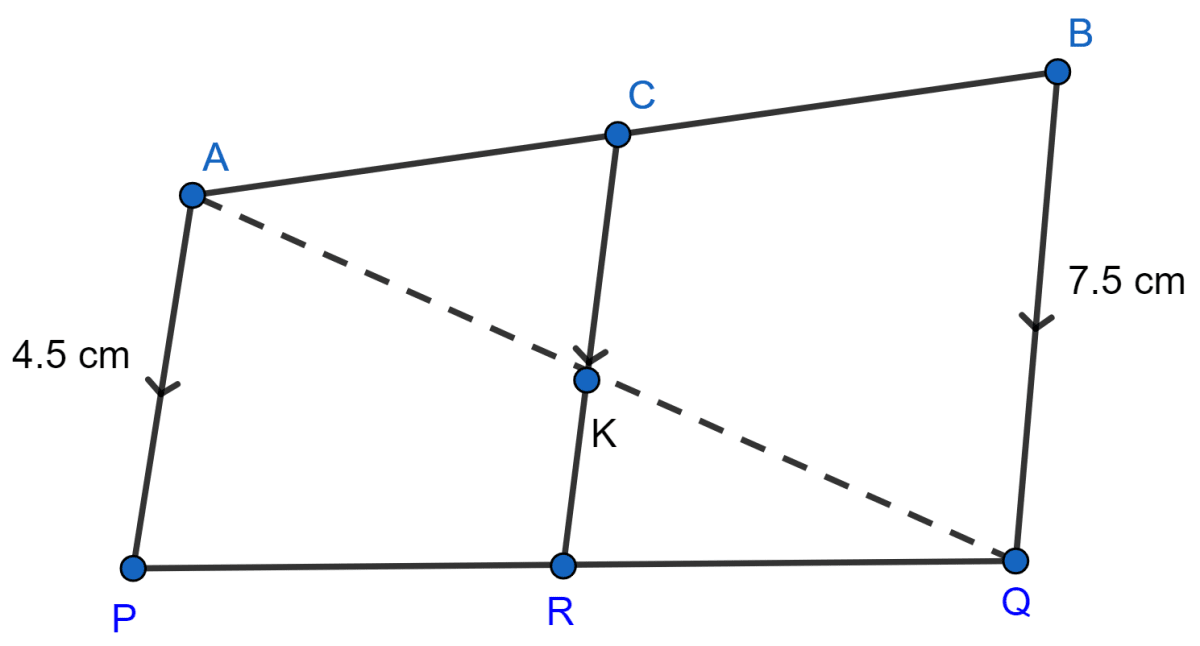
In the given figure, if AC = 3 cm and CB = 6 cm, find the length of CR.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO : OD = 4 : 7, find :
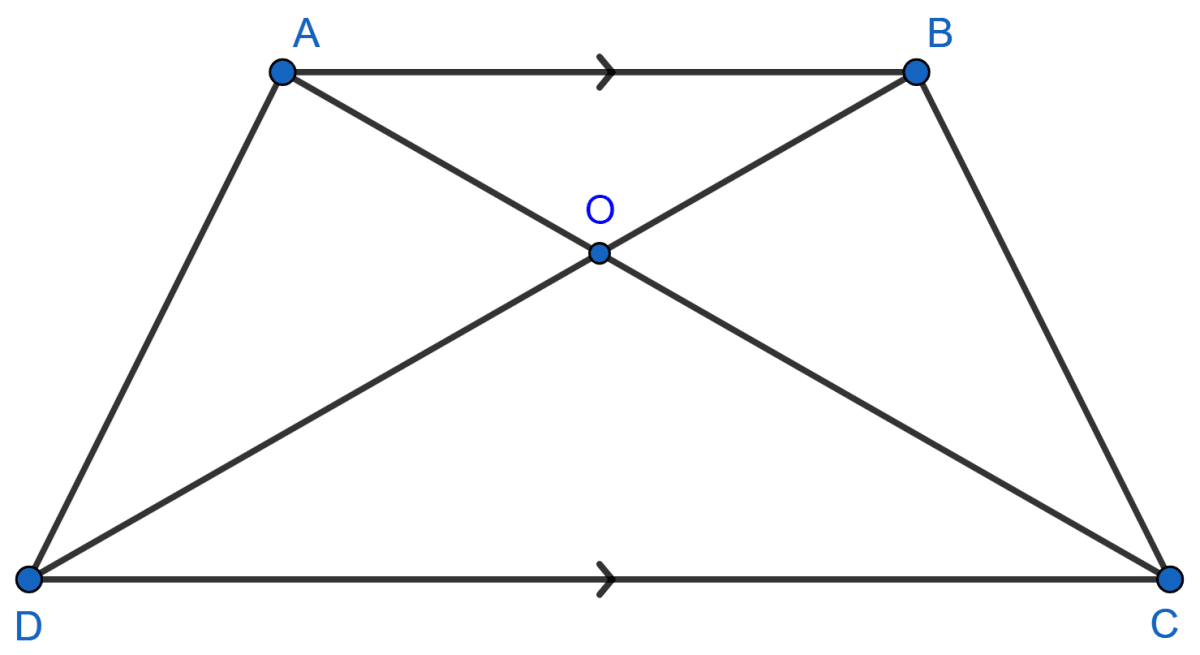
(i) △AOD : △AOB
(ii) △AOB : △ACB
(iii) △DOC : △AOB
(iv) △ABD : △BOC