Mathematics
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO : OD = 4 : 7, find :
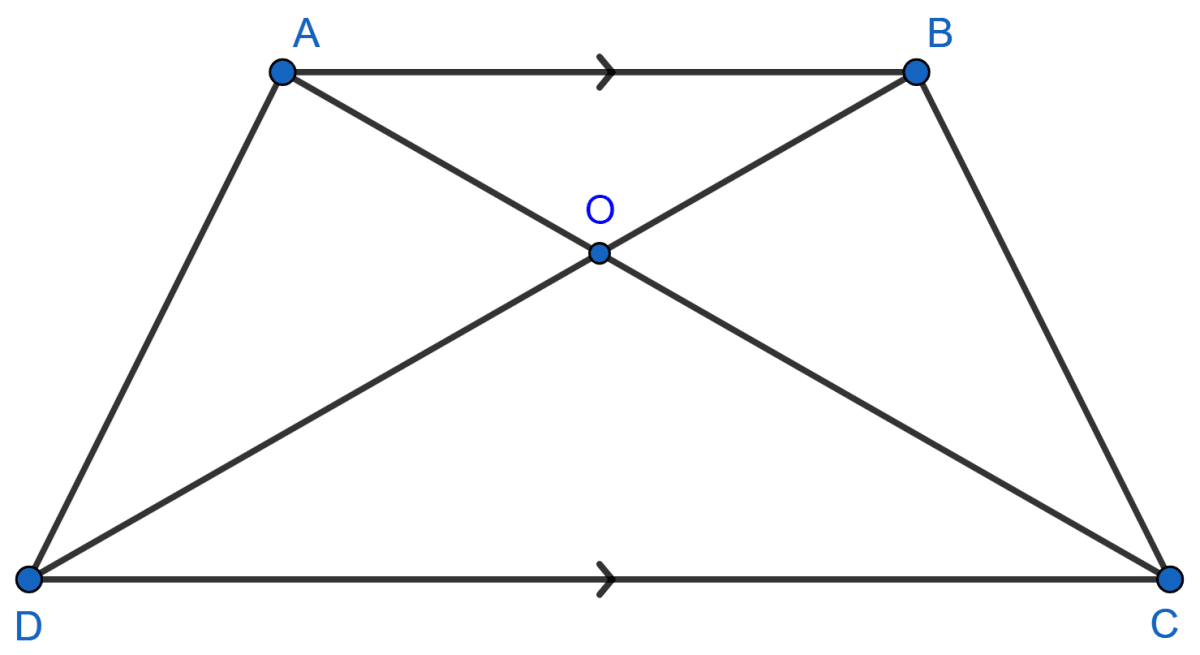
(i) △AOD : △AOB
(ii) △AOB : △ACB
(iii) △DOC : △AOB
(iv) △ABD : △BOC
Similarity
21 Likes
Answer
(i) Given,
⇒ BO : OD = 4 : 7
⇒ OD : OB = 7 : 4
Since,
△AOD and △AOB have common vertex at A and their bases OD and OB are along the same straight line.
.
Hence, △AOD : △AOB = 7 : 4.
(ii) Since,
△AOB and △ACB have common vertex at A and their bases AO and AC are along the same straight line.
Hence, △AOB : △ACB = 4 : 11.
(iii) Given,
BO : OD = 4 : 7
In △AOB and △DOC
∠AOB = ∠COD [Vertically opposite angles are equal]
∠ABO = ∠ODC [Alternate angles are equal]
∴ △AOB ~ △DOC [By AA axiom]
By area theorem,
Ratio of area of two similar triangles is equal to the square of the ratio of the corresponding sides.
Hence, △DOC : △AOB = 49 : 16.
(iv) Given,
BO : OD = 4 : 7
Since,
△ABD and △BOC have common vertex at B and their bases BD and OB are along the same straight line.
Hence, △ABD : △BOC = 11 : 4.
Answered By
12 Likes
Related Questions
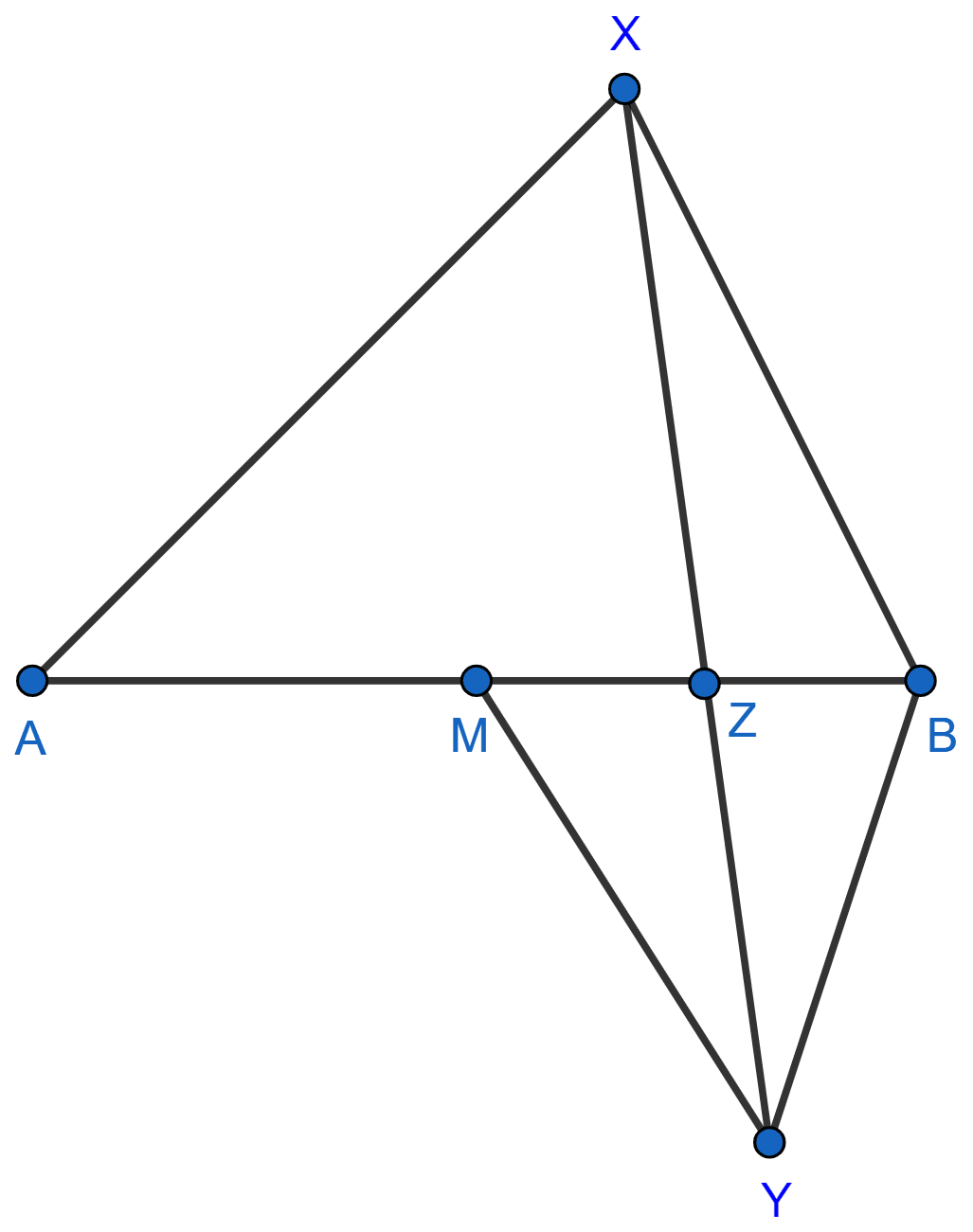
M is the mid-point of a line segment AB; AXB and MYB are equilateral triangles on opposite sides of AB; XY cuts AB at Z. Prove that : AZ = 2ZB.
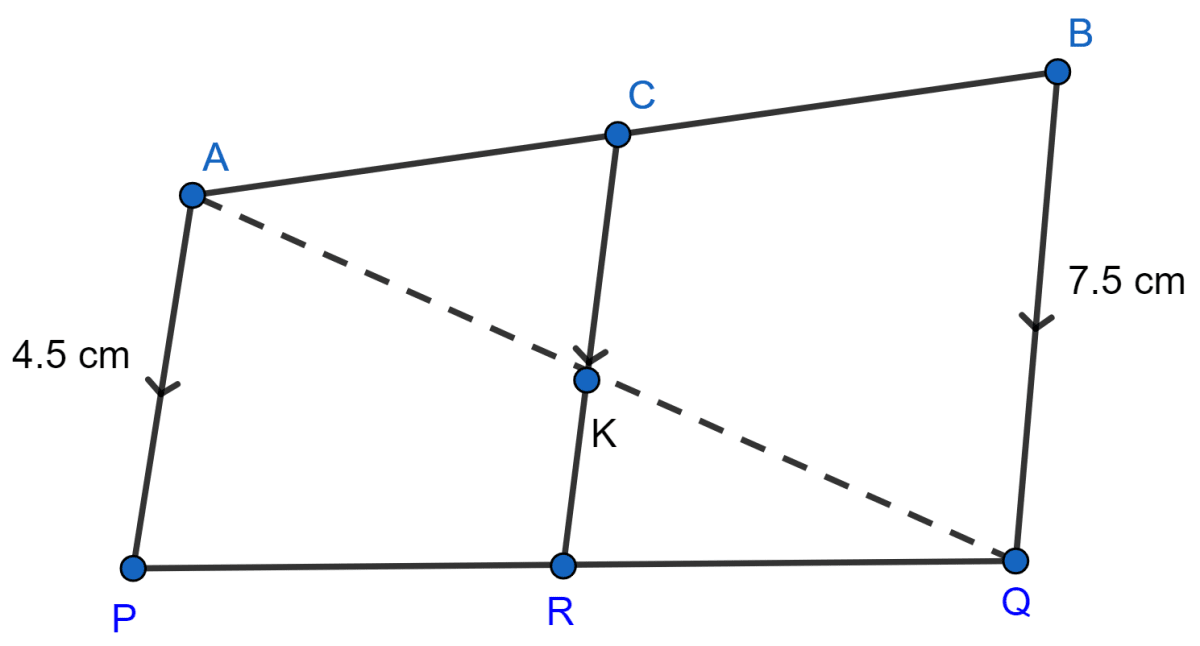
In the given figure, if AC = 3 cm and CB = 6 cm, find the length of CR.
A model of a ship is made to a scale of 1 : 160. Find :
(i) the length of the ship, if the length of its model is 1.2 m
(ii) the area of the deck of the ship , if the area of deck of its model is 1.2 m2.
(iii) the volume of the ship, if the volume of its model is 1.2 m3.
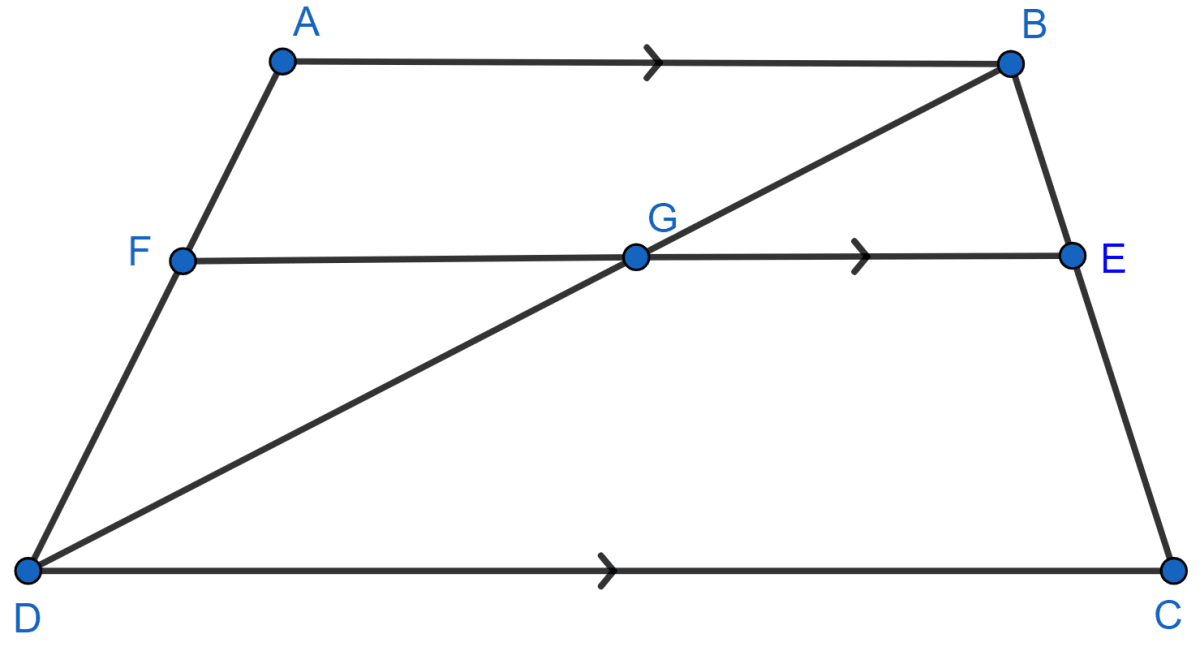
In trapezium ABCD, AB || DC and DC = 2AB. EF drawn parallel to AB cuts AD in F and BC in E such that 4 BE = 3EC. Diagonal DB intersects FE at point G. Prove that : 7EF = 10AB.