Mathematics
A model of a ship is made to a scale of 1 : 160. Find :
(i) the length of the ship, if the length of its model is 1.2 m
(ii) the area of the deck of the ship , if the area of deck of its model is 1.2 m2.
(iii) the volume of the ship, if the volume of its model is 1.2 m3.
Similarity
14 Likes
Answer
Given,
Scale of model = 1 : 160
Scale factor (k) =
(i) By formula,
⇒ Length of model = Scale factor × Length of ship
⇒ 1.2 = × Length of ship
⇒ Length of ship = 1.2 × 160 = 192 m.
Hence, length of ship = 192 m.
(ii) By formula,
⇒ Area of model = (Scale factor)2 × Area of ship
⇒ 1.2 = × Area of ship
⇒ 1.2 = × Area of ship
⇒ Area of ship = 1.2 × 160 × 160 = 30720 m2.
Hence, area of ship = 30720 m2.
(iii) By formula,
⇒ Volume of model = (Scale factor)3 × Volume of ship
⇒ 1.2 = × Volume of ship
⇒ 1.2 = × Volume of ship
⇒ Volume of ship = 1.2 × 160 × 160 × 160 = 49,15,200 m3.
Hence, volume of ship = 49,15,200 m3.
Answered By
8 Likes
Related Questions
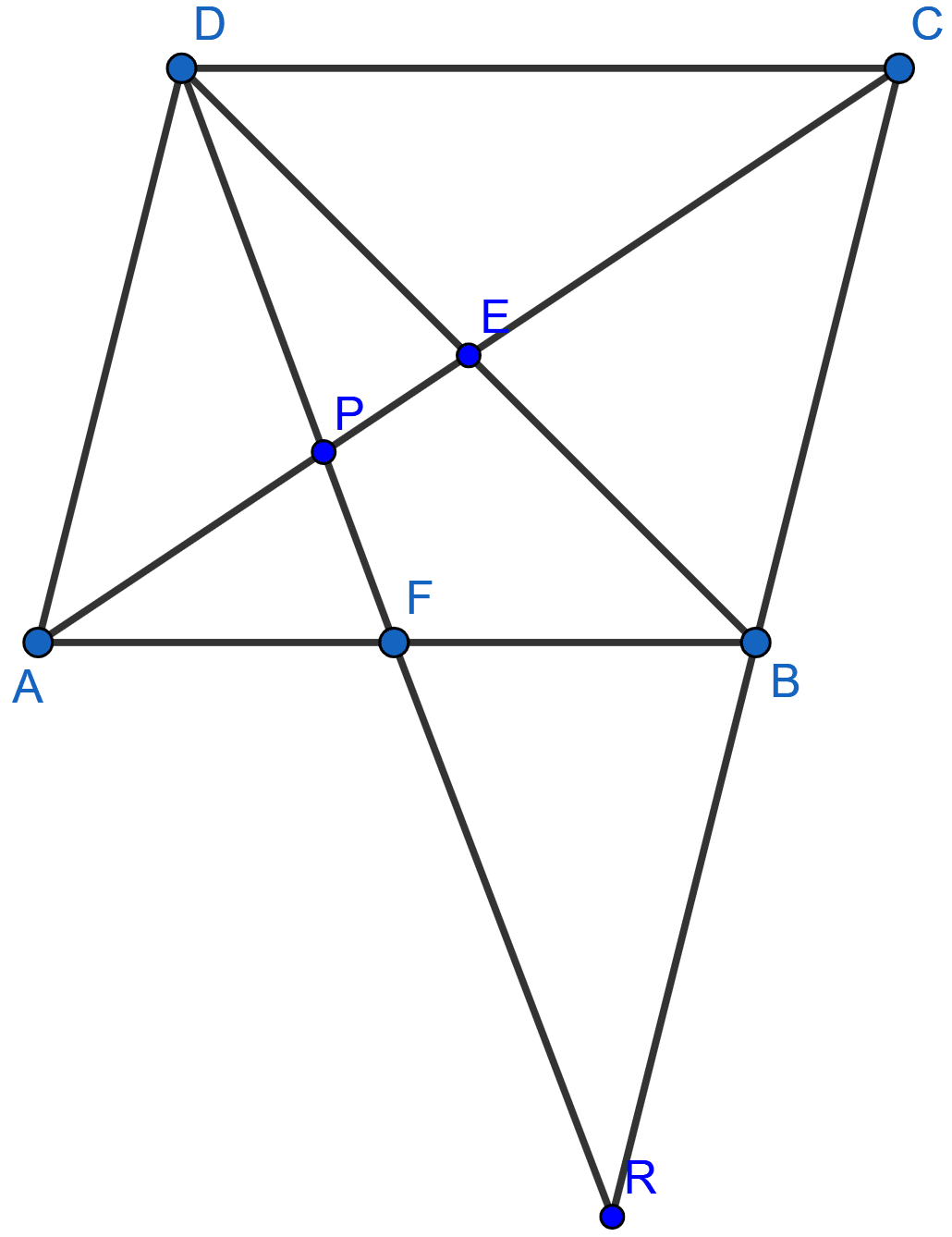
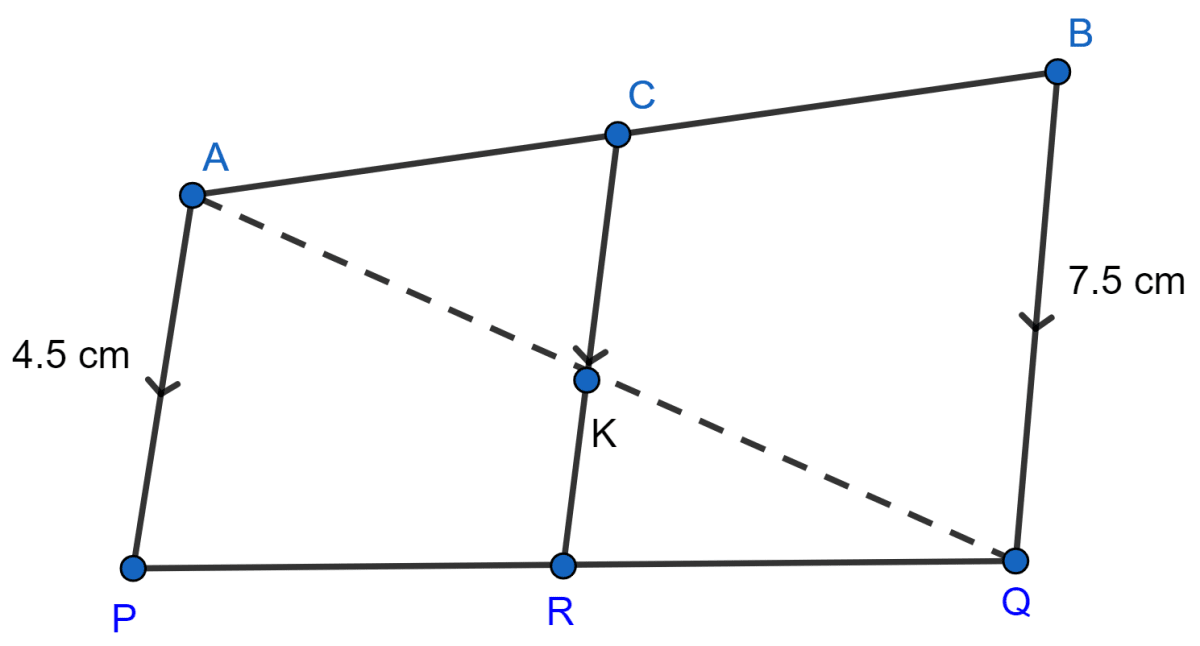
In the given figure, if AC = 3 cm and CB = 6 cm, find the length of CR.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO : OD = 4 : 7, find :
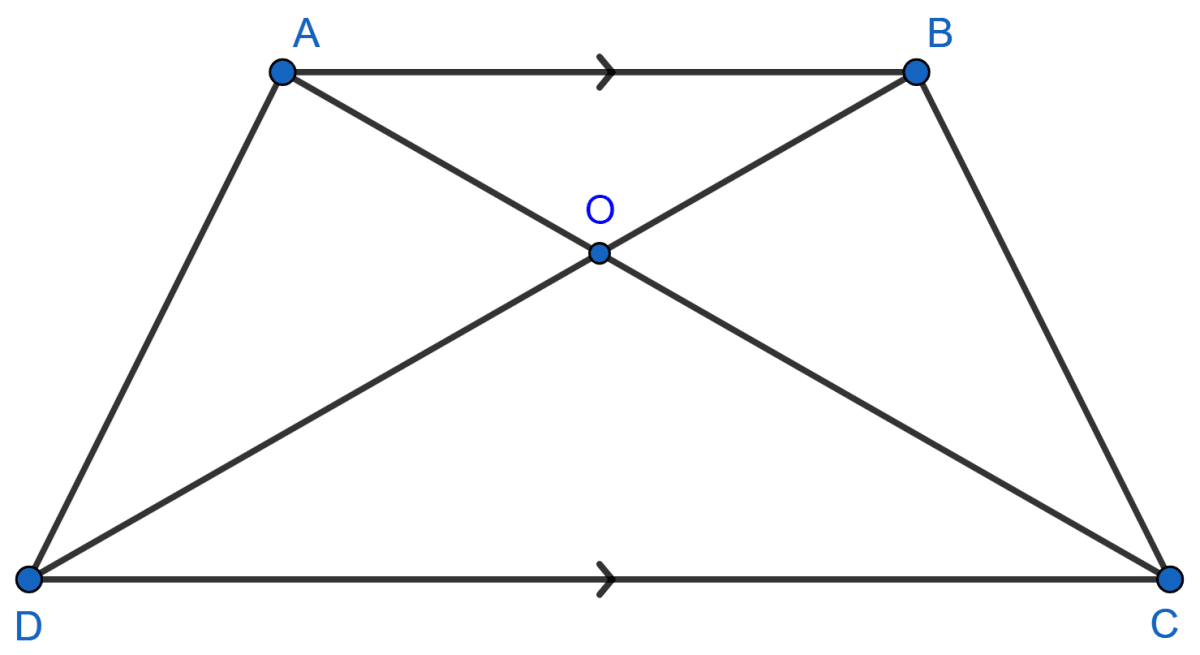
(i) △AOD : △AOB
(ii) △AOB : △ACB
(iii) △DOC : △AOB
(iv) △ABD : △BOC
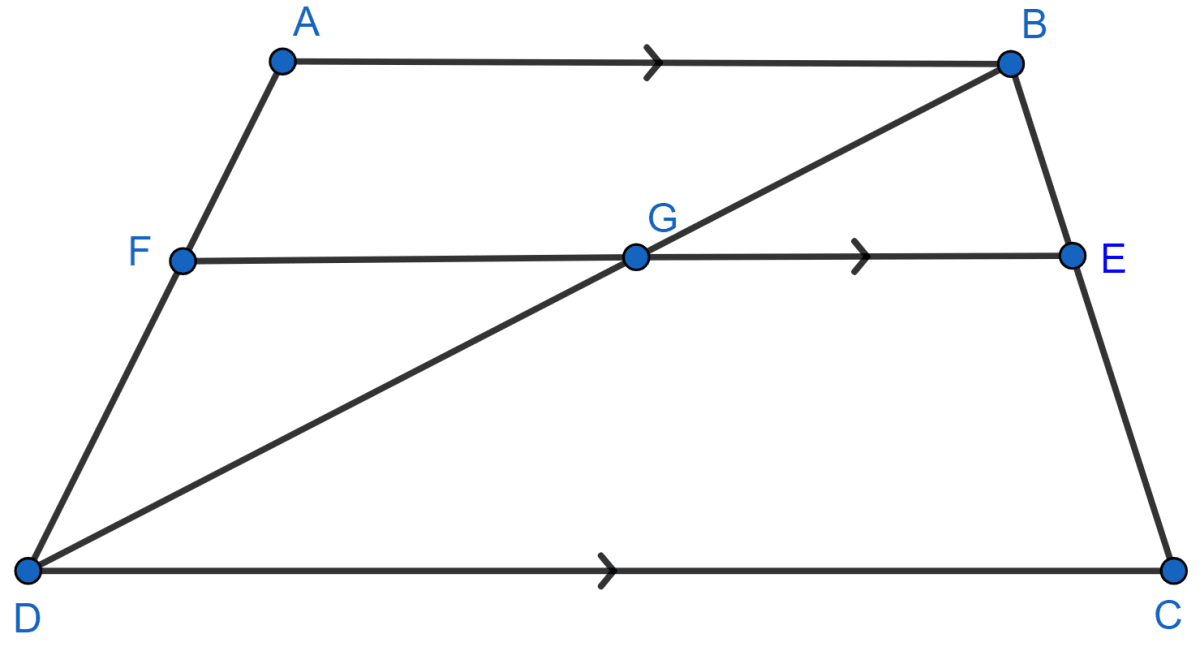
In trapezium ABCD, AB || DC and DC = 2AB. EF drawn parallel to AB cuts AD in F and BC in E such that 4 BE = 3EC. Diagonal DB intersects FE at point G. Prove that : 7EF = 10AB.
Given : ABCD is a rhombus, DPR and CBR are straight lines.
Prove that :
DP × CR = DC × PR.