Mathematics
A man covers a distance of 100 km, travelling with a uniform speed of x km/hr. Had the speed been 5 km/hr more it would have taken 1 hour less. Find x the original speed.
Quadratic Equations
ICSE 2023
7 Likes
Answer
In first case :
Distance = 100 km
Speed = x km/hr
Time =
In second case :
Distance = 100 km
Speed = (x + 5) km/hr
Time =
According to question,
The difference between the time taken between first and second case is 1 hour.
Since, speed cannot be negative.
∴ x = 20 km/hr.
Hence, original speed = 20 km/hr.
Answered By
4 Likes
Related Questions
A and B are two points on the x-axis and y-axis respectively.
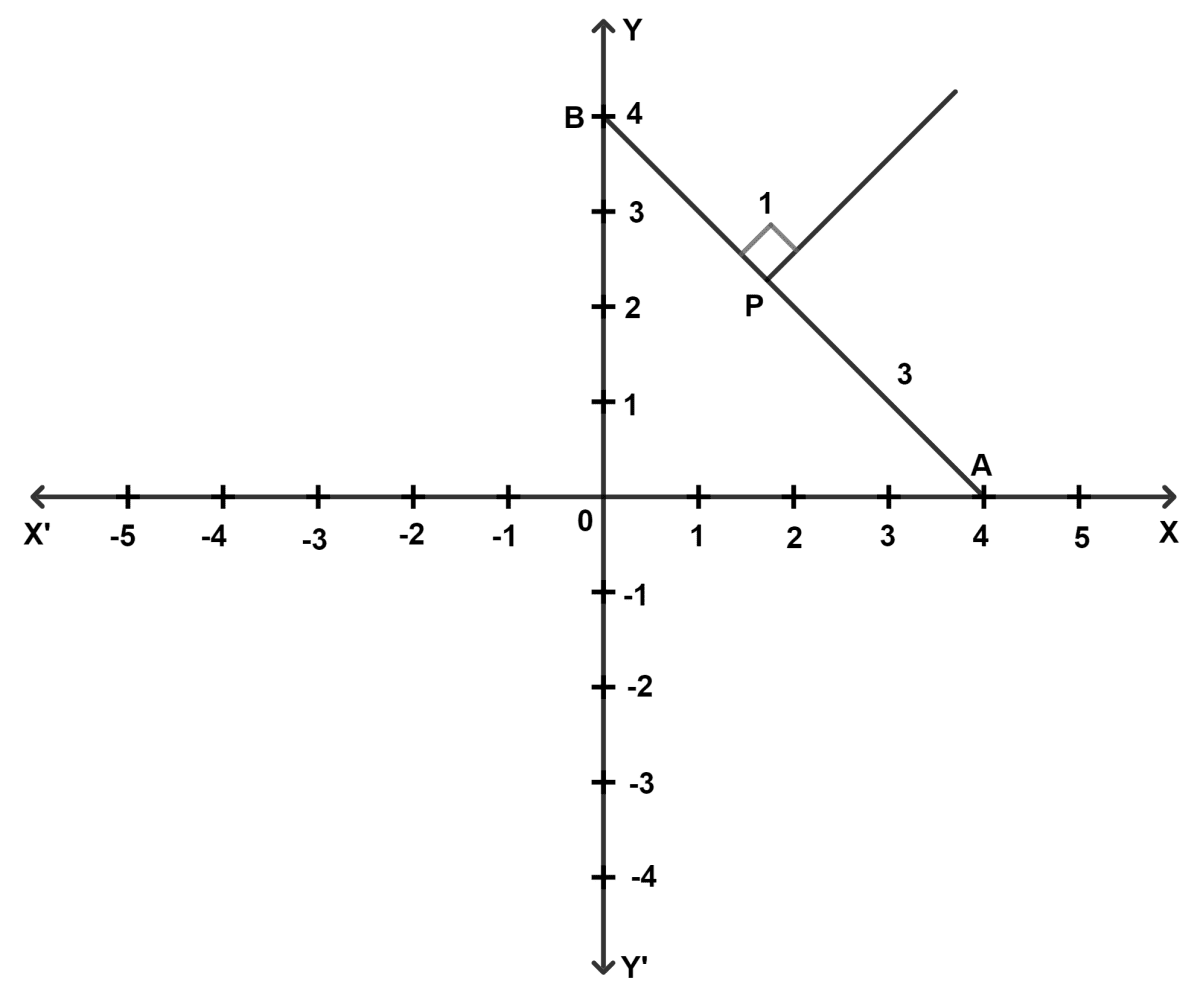
(a) Write down the co-ordinates of A and B.
(b) P is a point on AB such that AP : PB = 3 : 1. Using section formula find the coordinates of point P.
(c) Find the equation of a line passing through P and perpendicular to AB.
A bag contains 25 cards, numbered through 1 to 25. A card is drawn at random. What is the probability that the number on the card drawn is :
(a) a multiple of 5
(b) a perfect square
(c) a prime number ?
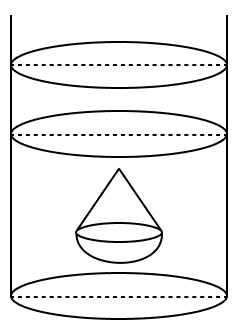
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height so that the solid is completely submerged in water. If the radius of the cylinder is 14 cm, find the rise in the water level.
The following table gives the marks scored by a set of students in an examination. Calculate the mean of the distribution by using the short cut method.
Marks Number of students (f) 0-10 3 10-20 8 20-30 14 30-40 9 40-50 4 50-60 2