Mathematics
O is centre of the circle, PB and PC are tangents and ∠BPC = 50°.
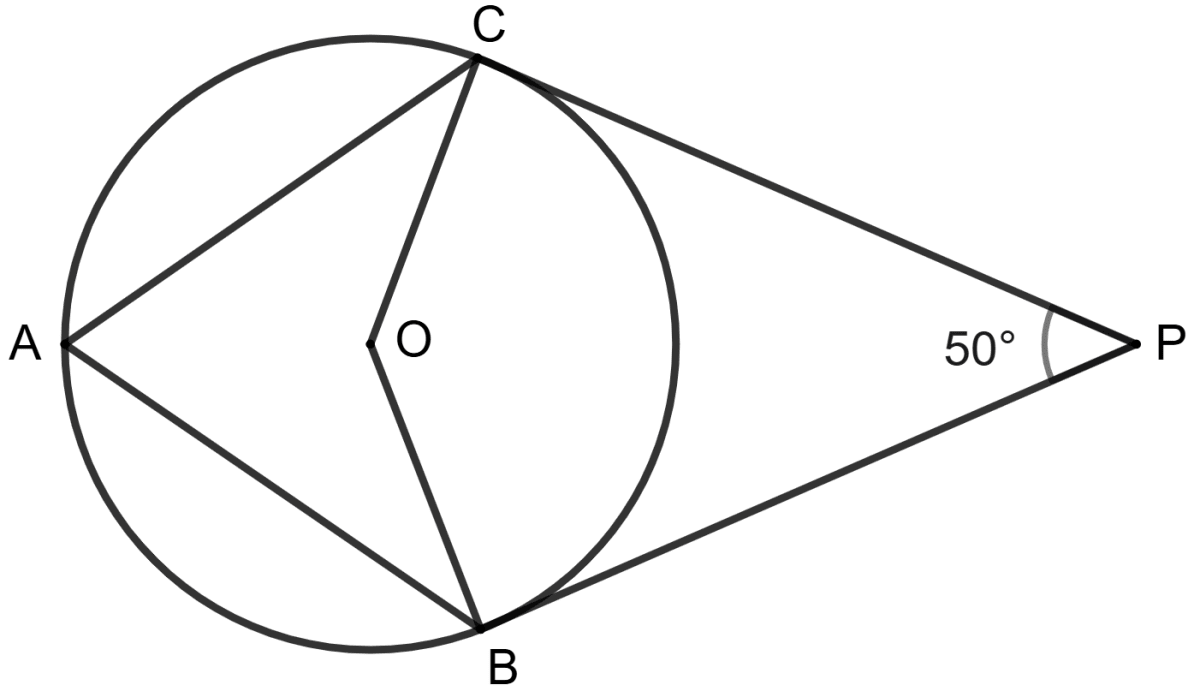
Statement (1): ∠BAC = ∠P = 50°
Statement (2): ∠BOC + 50° = 180°
⇒ ∠BOC = 130°
∴ ∠BAC = 65°
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Circles
2 Likes
Answer
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OB ⊥ BP and OC ⊥ CP
⇒ ∠OBP = 90° and ∠OCP = 90°
OCPB is a quadrilateral.
∴ ∠OBP + ∠BPC + ∠OCP + ∠BOC = 360°
⇒ 90° + 50° + 90° + ∠BOC = 360°
⇒ 230° + ∠BOC = 360°
⇒ ∠BOC = 360° - 230°
⇒ ∠BOC = 130°
We know that,
The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
∴ ∠BOC = 2 x ∠BAC
⇒ 130° = 2 x ∠BAC
⇒ ∠BAC = = 65°.
So, Statement 1 is false, and statement 2 is true.
Hence, option 4 is the correct option.
Answered By
1 Like
Related Questions
Chords AD and BC one produce meet at exterior point P.
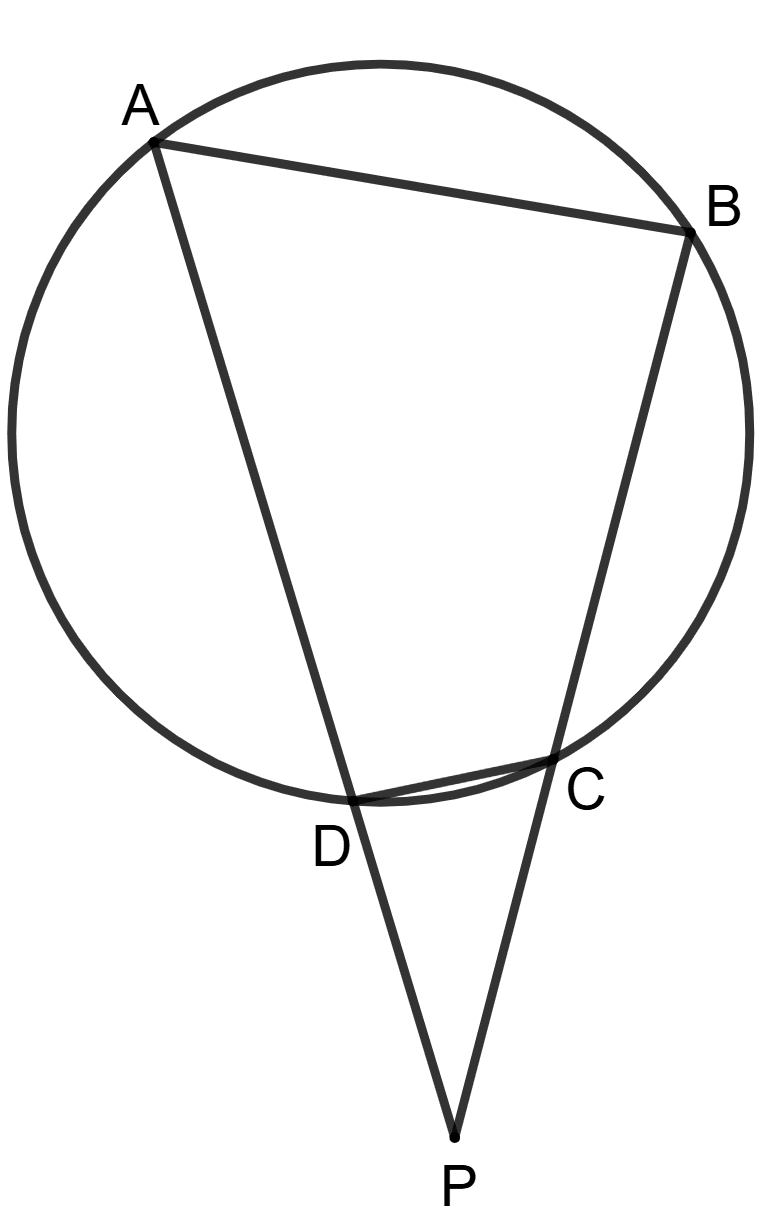
Assertion(A): PD x AD = PC x BC.
Reason(R): In triangles PAB and PCD.
∠PAB = ∠PCD ⇒ ΔPAB ∼ ΔPCD
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Two circles touch each other externally at point P. OA and OB are the tangent of the two circles (as shown) and OA = 10 cm.
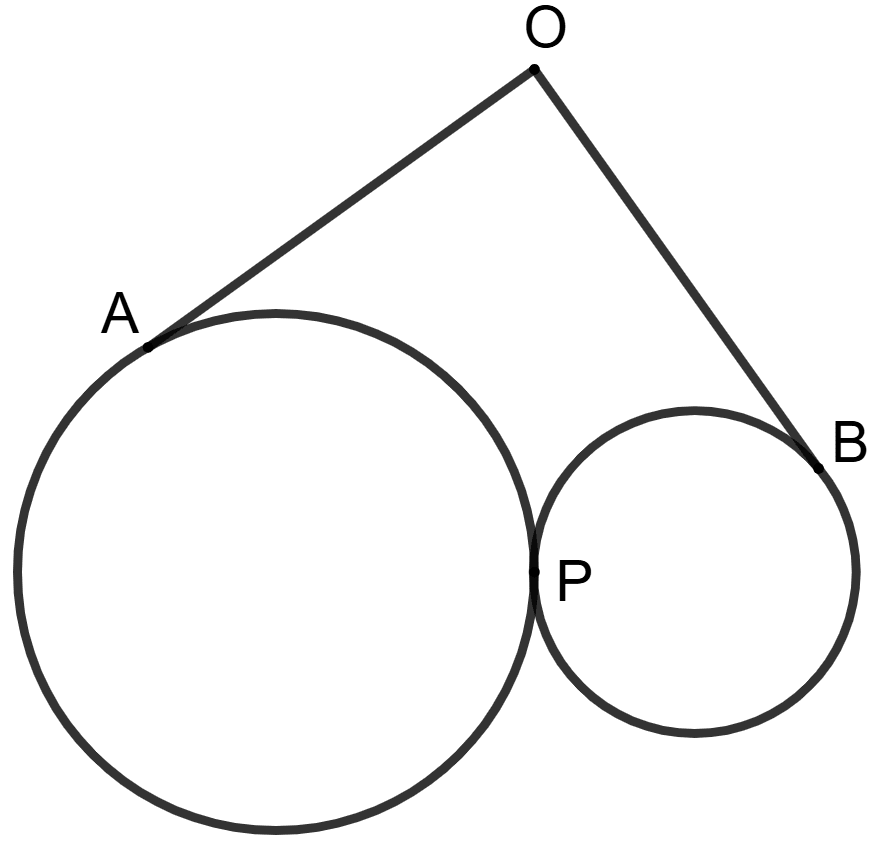
Statement (1): OB = 10 cm.
Statement (2): On joining O and P, tangent OP = tangent OA and tangent OP = tangent OB
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.