Mathematics
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
Circles
24 Likes
Answer
Let there be a circle with center O and radius r. AB and CD are two chords of this circle. OM < ON where OM ⊥ AB and ON ⊥ CD.
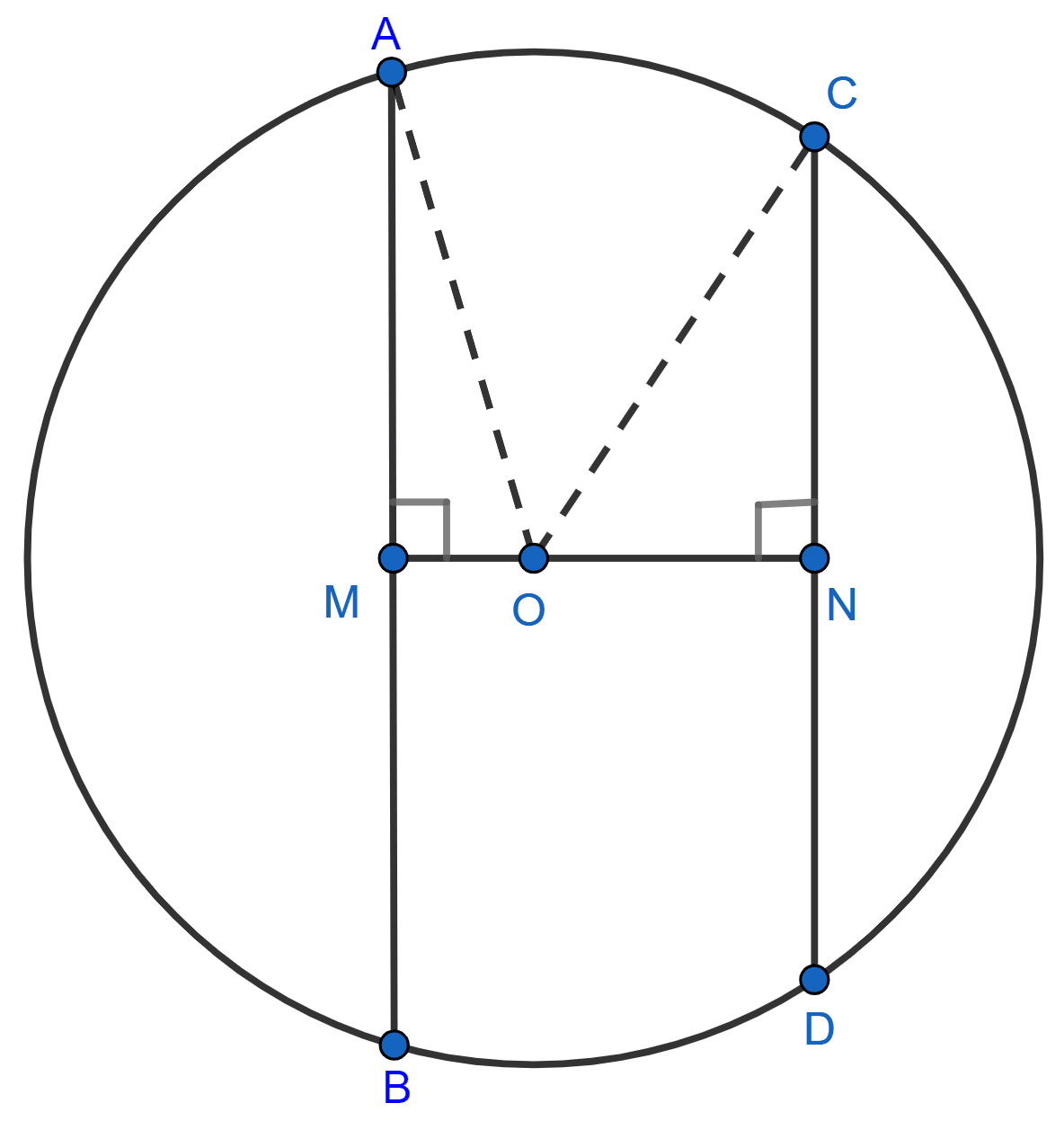
To prove: AB > CD
We know that,
The perpendicular from the centre of a circle to a chord bisects the chord.
∴ AM = and CN =
Join OA and OC.
In right angle triangle OAM,
⇒ OA2 = AM2 + OM2
⇒ AM2 = OA2 - OM2 ….. (1)
In right angle triangle ONC,
⇒ OC2 = CN2 + ON2
⇒ CN2 = OC2 - ON2 ….. (2)
OM < ON
⇒ OM2 < ON2
⇒ -OM2 > -ON2
⇒ OA2 - OM2 > OC2 - ON2 [∵ OA = OC]
⇒ AM2 > CN2 [From (1) and (2)]
⇒ >
⇒ AB2 > CD2
⇒ AB2 > CD2
⇒ AB > CD
Hence proved that, of any two chords of a circle, the greater chord is nearer to the centre.
Answered By
12 Likes
Related Questions
Two circles touch each other externally at point P. OA and OB are the tangent of the two circles (as shown) and OA = 10 cm.
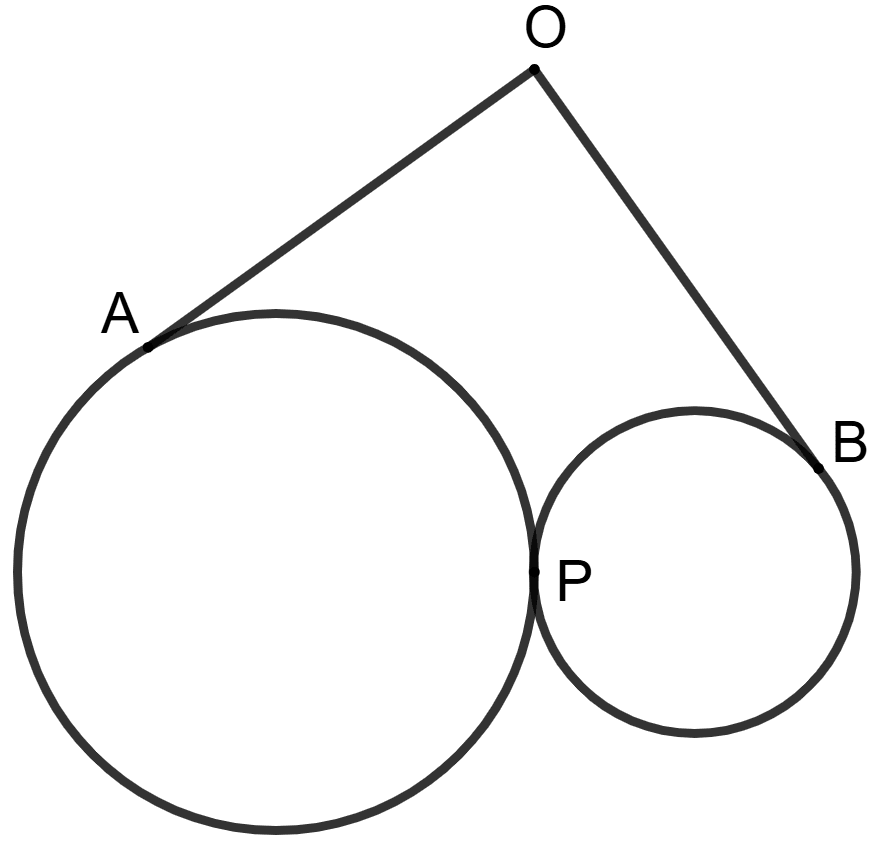
Statement (1): OB = 10 cm.
Statement (2): On joining O and P, tangent OP = tangent OA and tangent OP = tangent OB
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
O is centre of the circle, PB and PC are tangents and ∠BPC = 50°.
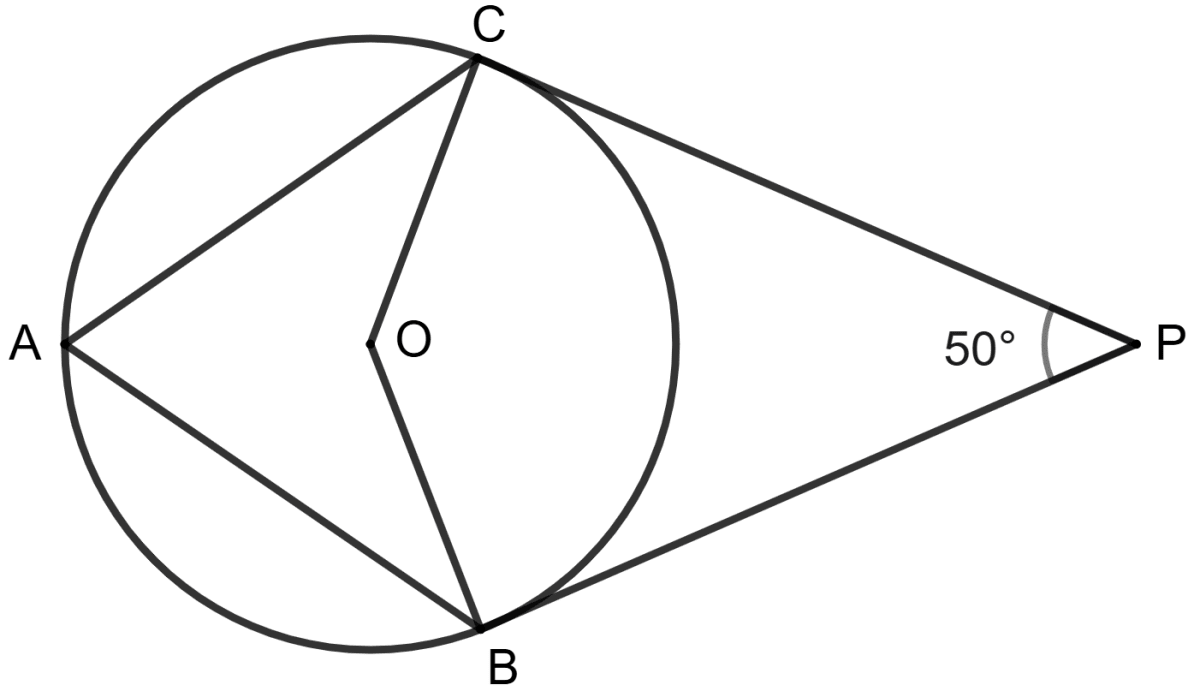
Statement (1): ∠BAC = ∠P = 50°
Statement (2): ∠BOC + 50° = 180°
⇒ ∠BOC = 130°
∴ ∠BAC = 65°
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
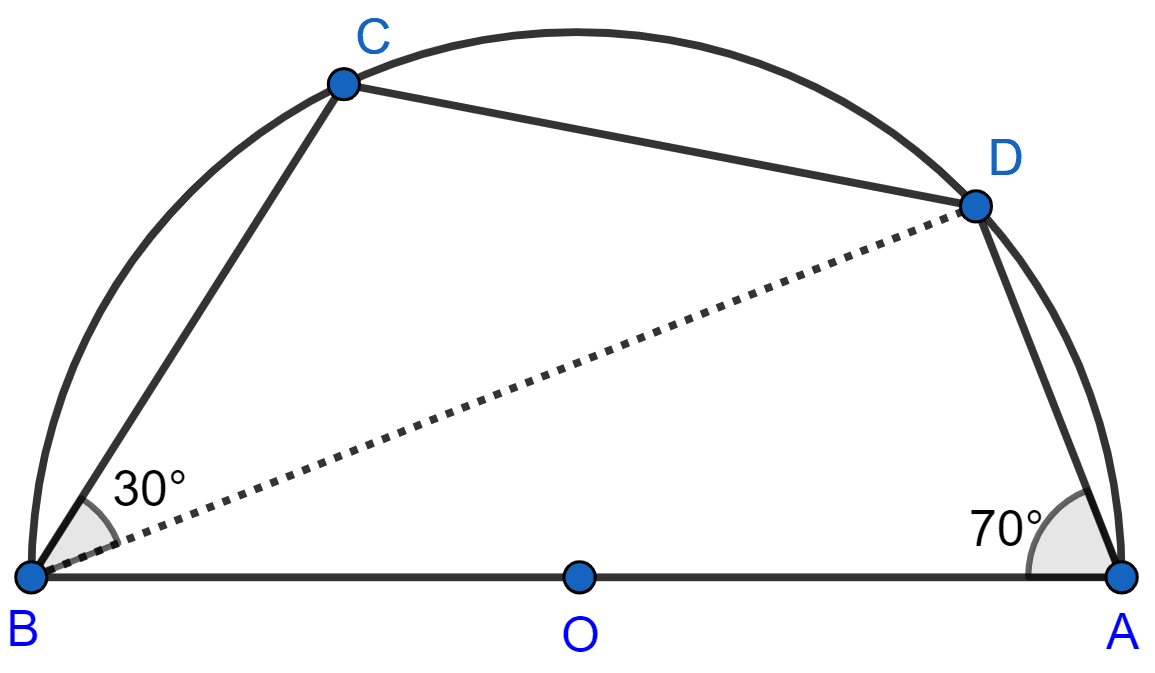
In the given figure, C and D are points on the semi-circle described on AB as diameter.
Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.