Mathematics
The perpendicular BD drawn from the vertex of a right triangle ABC.
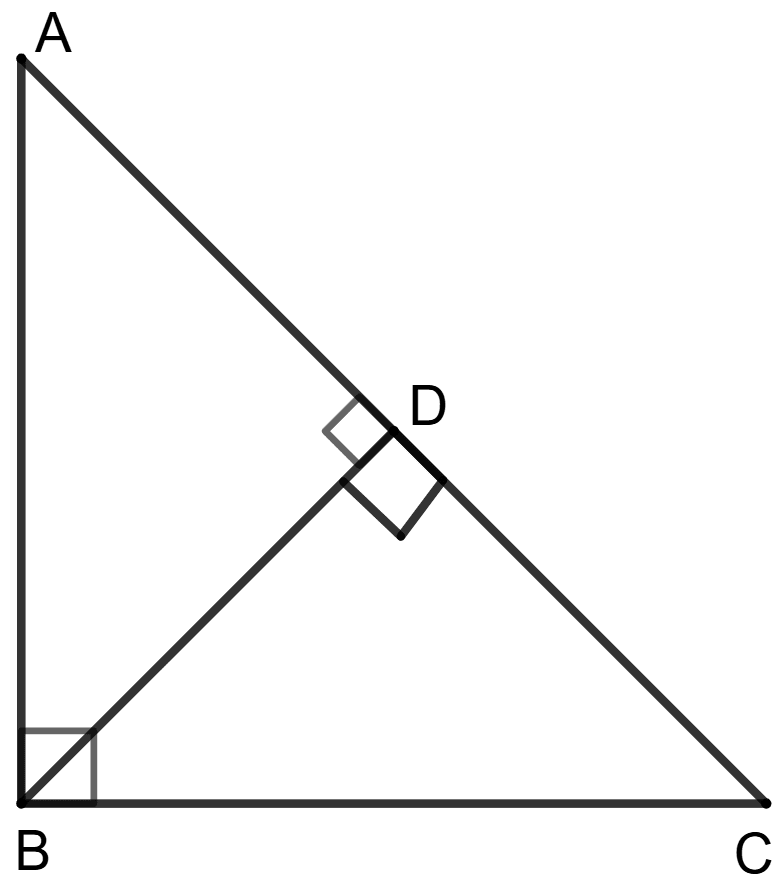
Assertion (A) : Triangles ABD and BCD are similar to each other.
Reason (R) : Triangles, which are similar to the same triangle, are similar to each other.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Similarity
5 Likes
Answer
In Δ ABC and Δ ABD,
⇒ ∠ABC = ∠ADB (Both are 90°)
⇒ ∠BAC = ∠BAD (Common angle)
∴ Δ ABC ∼ Δ ADB (By AA postulate) ………. (1)
Similarly, in Δ ABC and Δ BDC,
⇒ ∠ABC = ∠BDC (Both are 90°)
⇒ ∠BCA = ∠BCD (Common angles)
∴ Δ ABC ∼ Δ BDC (By AA postulate) ………. (2)
As,
Triangles, which are similar to the same triangle, are similar to each other.
From equation (1) and (2), we get :
Δ ADB ∼ Δ BDC
∴ Both A and R are true and R is correct reason for A.
Hence, option 3 is the correct option.
Answered By
2 Likes
Related Questions
In △ABD, C is a point on side BD such that ∠ACD = ∠BAD. Is △BAD similar to triangle ACD? If yes, then which axiom is satisfied :
Yes, ASA
Yes, SAS
Yes, AA
No

The model of a ship is made to a scale of 3 : 500. If the length of the model is 1.5 m, the length of ship is :
750 m
1000 m
450 m
250 m
Δ ABC and Δ PQR are congruent to each other.
Assertion (A) : Triangles ABC and PQR are similar to each other.
Reason (R) : Two similar triangles are congruent to each other.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Δ ABC is reflected in origin to get Δ A'B'C'.
Statement (1) : Δ ABC is congruent to Δ A'B'C'.
Statement (2) : The two triangles are similar to each other.
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.