The perpendicular BD drawn from the vertex of a right triangle ABC.

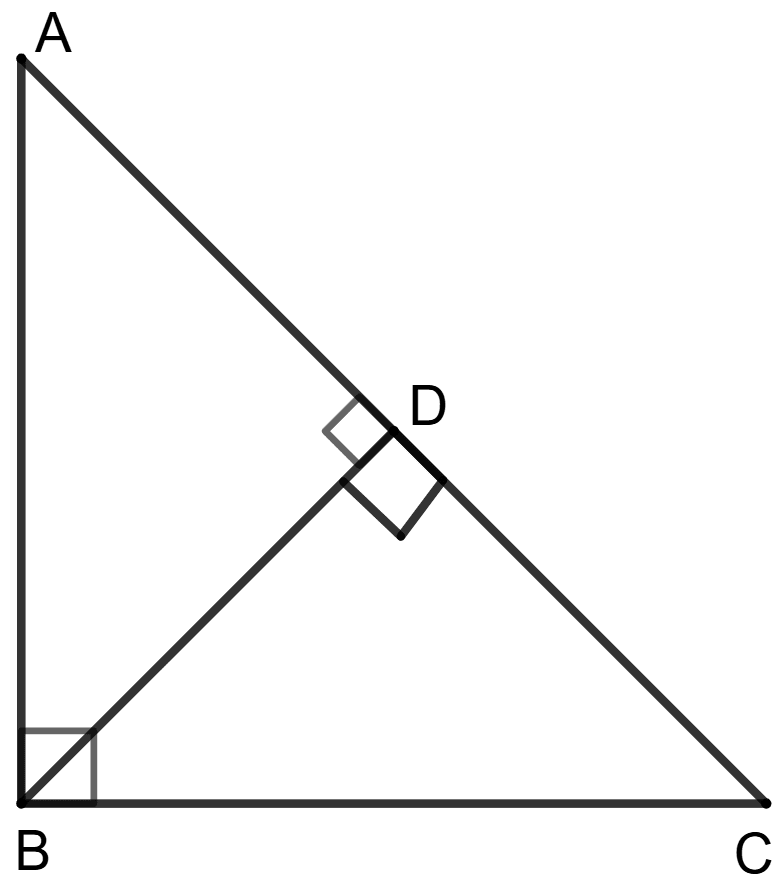
Assertion (A) : Triangles ABD and BCD are similar to each other.

Reason (R) : Triangles, which are similar to the same triangle, are similar to each other.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Δ ABC and Δ PQR are congruent to each other.

Assertion (A) : Triangles ABC and PQR are similar to each other.

Reason (R) : Two similar triangles are congruent to each other.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Two similar triangles ABC and DEF such that area of Δ ABC = 64 sq. unit and area of Δ DEF = 121 sq. unit.

Statement (1) : $\dfrac{\text{Perimeter of Δ DEF}}{\text{Perimeter of Δ ABC}} = \dfrac{8}{11}$.

Statement (2) : The ratio of perimeters of two similar triangles is equal to the ratio of their areas.

1. Both the statement are true.

2. Both the statement are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

In triangle ABC, AD : DB = 2 : 3, DE is parallel to BC.

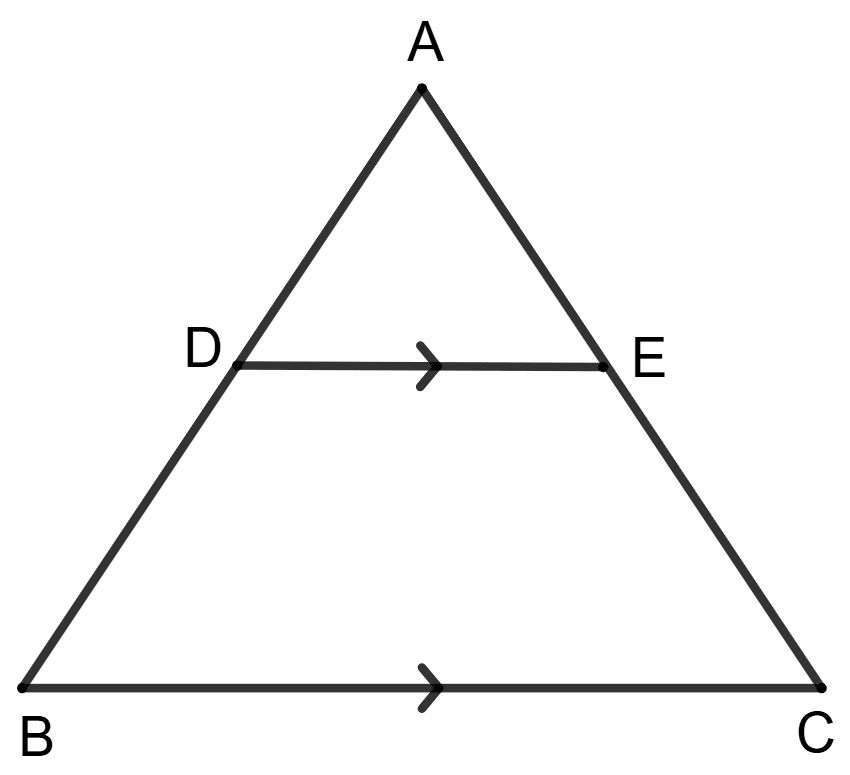
Assertion (A) : $\dfrac{\text{DE}}{\text{BC}} = \dfrac{\text{AD}}{\text{BD}} = \dfrac{2}{3}$.

Reason (R) : $\dfrac{\text{DE}}{\text{BC}} = \dfrac{\text{AD}}{\text{AB}} = \dfrac{2}{5}$.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.