Mathematics
Two similar triangles ABC and DEF such that area of Δ ABC = 64 sq. unit and area of Δ DEF = 121 sq. unit.
Statement (1) : .
Statement (2) : The ratio of perimeters of two similar triangles is equal to the ratio of their areas.
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Similarity
6 Likes
Answer
Given, △ ABC ∼ △ DEF.
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Since, corresponding sides of similar triangle are proportional.
We know that,
For any two or more equal ratios, each ratio is equal to the ratio between sum of their antecedents and sum of their consequents.
So, statement 1 is false.
The ratio of perimeters of two similar triangles is equal to the ratio of their corresponding sides.
So, statement 2 is false.
Hence, option 2 is the correct option.
Answered By
2 Likes
Related Questions
Δ ABC and Δ PQR are congruent to each other.
Assertion (A) : Triangles ABC and PQR are similar to each other.
Reason (R) : Two similar triangles are congruent to each other.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Δ ABC is reflected in origin to get Δ A'B'C'.
Statement (1) : Δ ABC is congruent to Δ A'B'C'.
Statement (2) : The two triangles are similar to each other.
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
In triangle ABC, AD : DB = 2 : 3, DE is parallel to BC.
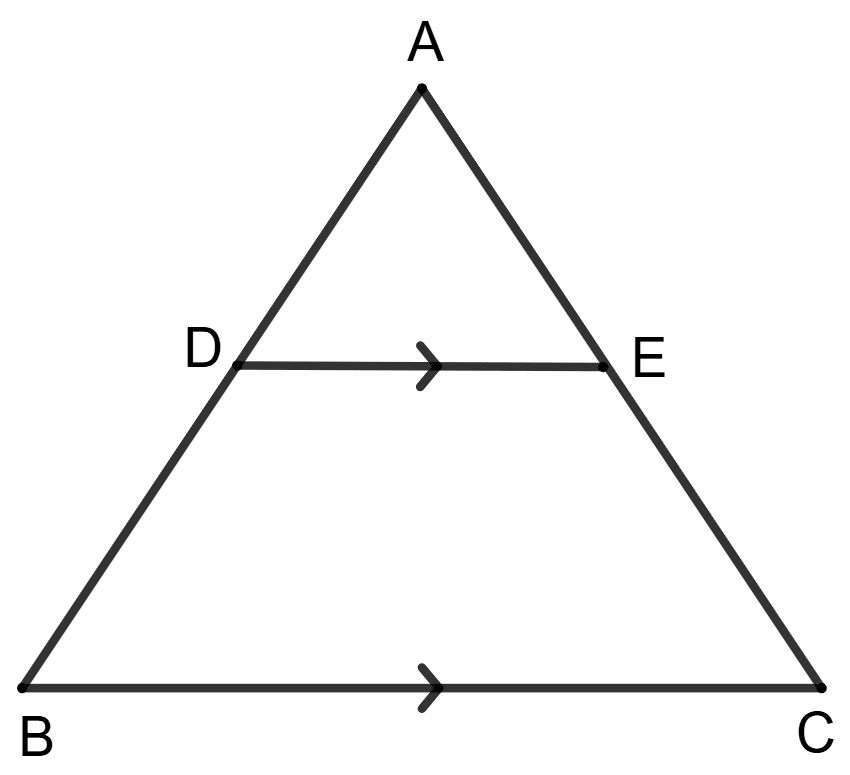
Assertion (A) : .
Reason (R) : .
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
In triangle ODQ, ∠Q = ∠BPO = 90° AB = 2 x OA, BC = 3 x OA and CD = 4 x OA.
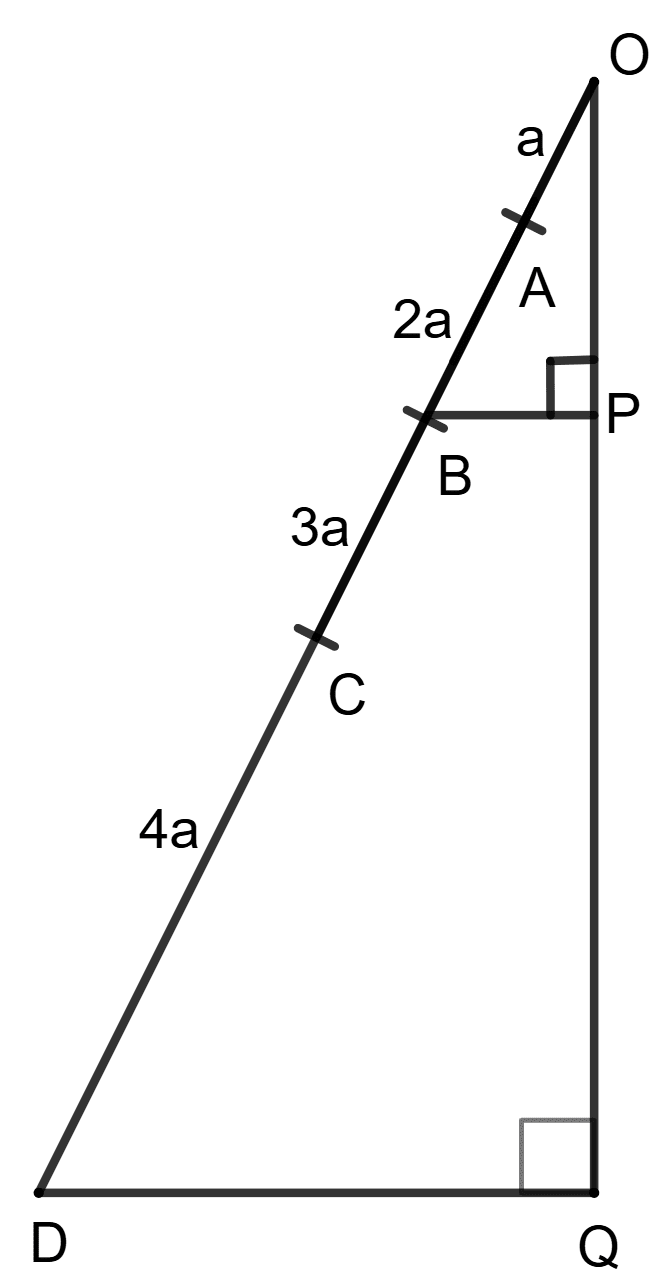
Assertion (A) : .
Reason (R) : Δ OBP - ODQ and .
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.