Physics
A person standing in front of a cliff fires a gun and hears its echo after 3s. If the speed of sound in air is 336 ms-1.
(a) Calculate the distance of the person from the cliff.
(b) After moving a certain distance from the cliff, he fires the gun again and this time the echo is heard 1.5 s later than the first. Calculate the distance that the person moved.
Sound
5 Likes
Answer
(a) Given,
Time taken to hear the echo = 3s
Speed of sound = 336 ms-1
So,
So, distance of the person from the cliff is 504 m.
(b) Given,
Time taken to hear the new echo = 3 s + 1.5 s = 4.5 s
So,
Distance moved by the person = 756 - 504 = 252 m
So, distance moved by the person is 252 m.
Answered By
3 Likes
Related Questions
The figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
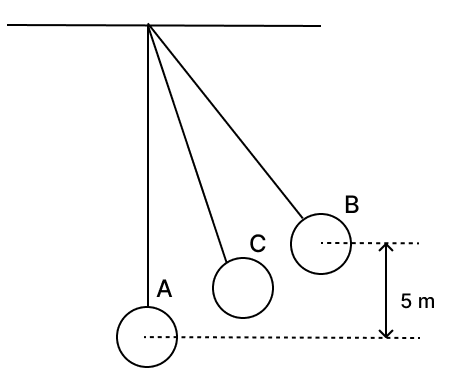
(a) What is the potential energy of the pendulum at the position В?
(b) What is the total mechanical energy at point C?
(c) What is the speed of the bob at the position A when released from B?
(Take g = 10 ms-2 and given that there is no loss of energy.)
A block and tackle system of pulleys has velocity ratio 4.
(a) Draw a labelled diagram of the system indicating clearly, the direction of the load and effort.
(b) Calculate the potential energy of the load 100 kgf lifted by this pulley to a height 5 m. (g = 10 ms-2)
The below picture shows a mother pushing her daughter sitting on a swing. The swing is going through the positions A, B, C where A and C are extreme positions and B is the mean position.

(a) Which is the right position i.e. at A, B or C, for the mother to give a constant periodic push to the swing every time in the forward direction to increase the amplitude of the swing?
(b) Name the phenomenon involved in this.
(c) Explain with this example how this phenomenon helps to increase the amplitude of the swing.
The circuit depicted in the figure is employed for studying Ohm's Law. Instead of using a standard resistor, a student opts for a glass tube filled with mercury (tube 1), connected to the circuit through two electrodes E1 & E2. He records the readings of the ammeter and voltmeter, thereby calculates the resistance. The student repeats the experiment by substituting tube 1 with tube 2, where the same amount of mercury fills the tube 2.
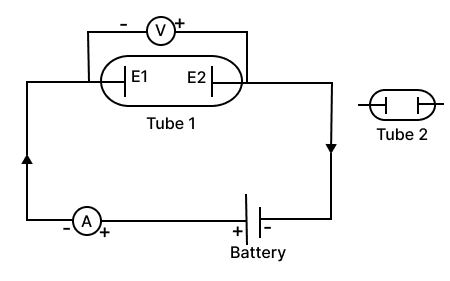
Neglecting internal resistance of the cell use (> or < or =) to compare
(a) the resistance in both the cases.
(b) the voltmeter readings in both the cases.
(c) the specific resistance in both the cases.