Physics
A person swings on a rope from a cliff that is 20 m high. How fast is the person moving at the lowest point of the swing? (Take g=10m/s-2)
Work, Energy & Power
32 Likes
Answer
As the person swings on a rope from a cliff of height h = 20 m then potential energy at the top gets converted into kinetic energy at the lowest point.
From conservation of energy,
Potential energy at top = Kinetic energy at lowest point
mgh = mv2
gh = v2
10 x 20 = v2
400 = v2
m/s
∴ The person is moving at a speed of 20 m/s at the lowest point of the swing.
Answered By
23 Likes
Related Questions
A stone of mass 500 g is thrown vertically upwards with a velocity of 15ms-1.
Calculate:
(a) the potential energy at the greatest height,
(b) the kinetic energy on reaching the ground
(c) the total energy at its half waypoint.
A metal ball of mass 2kg is allowed to fall freely from rest from a height of 5m above the ground.
- Taking g = 10ms-1, calculate:
- the potential energy possessed by the ball when it is initially at rest.
- the kinetic energy of the ball just before it hits the ground?
- What happens to the mechanical energy after the ball hits the ground and comes to rest?
- Taking g = 10ms-1, calculate:
The diagram given below shows a ski jump. A skier weighing 60kgf stands at A at the top of ski jump. He moves from A and takes off for his jump at B.
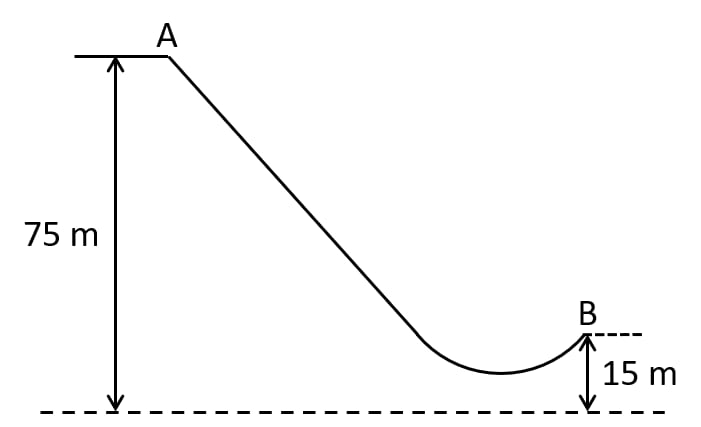
(a) Calculate the change in the gravitational potential energy of the skier between A and B.
(b) If 75% of the energy in part (a) becomes the kinetic energy at B, calculate the speed at which the skier arrives at B.
(Take g = 10 ms-2).
(c) Does total mechanical energy change during the ski jump?
A hydroelectric power station takes its water from a lake whose water level is 50m above the turbine. Assuming an overall efficiency of 40%, calculate the mass of water which must flow through the turbine each second to produce power output of 1MW. (Take g = 10 m s-2).