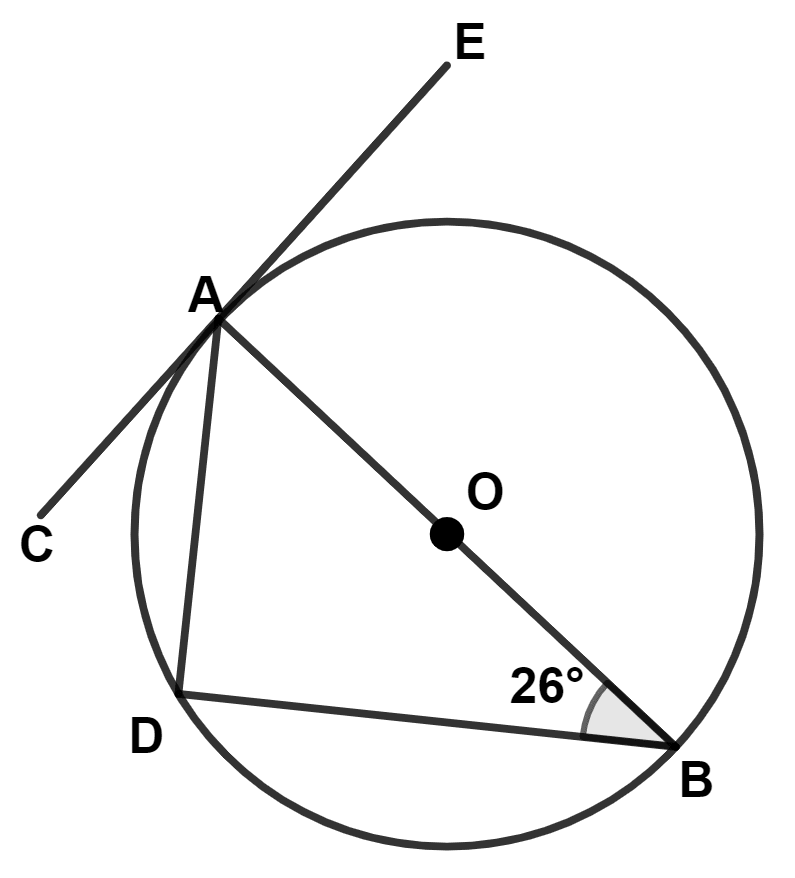
In the given figure O, is the center of the circle. CE is a tangent to the circle at A. If ∠ABD = 26°, then find :

(a) ∠BDA

(b) ∠BAD

(c) ∠CAD

(d) ∠ODB

Solve the following quadratic equation :

x² + 4x - 8 = 0.

Give your answer correct to one decimal place.

Use graph sheet to answer this question. Take 2 cm = 1 unit along both the axes.

(a) Plot A, B, C where A(0, 4), B(1, 1) and C(4, 0).

(b) Reflect A and B on the x-axis and name them as E and D respectively.

(c) Reflect B through the origin and name it F. Write down the coordinates of F.

(d) Reflect B and C on the y-axis and name them as H and G respectively.

(e) Join points A, B, C, D, E, F, G, H and A in order and name the closed figure formed.

If $A = \begin{bmatrix$}[r] 1 & 3 \ 2 & 4 \end{bmatrix}, B = \begin{bmatrix}[r] 1 & 2 \ 2 & 4 \end{bmatrix}, C = \begin{bmatrix}[r] 4 & 1 \ 1 & 5 \end{bmatrix} \text{ and } I = \begin{bmatrix}[r] 1 & 0 \ 0 & 1 \end{bmatrix}. Find A(B + C) - 14I.