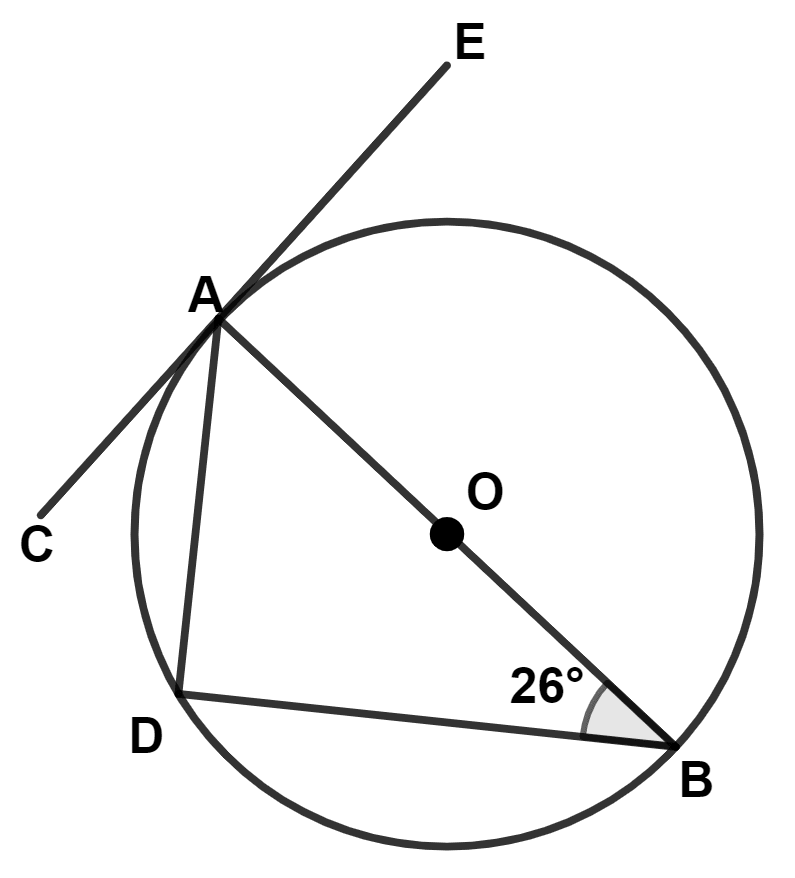
In the given figure O, is the center of the circle. CE is a tangent to the circle at A. If ∠ABD = 26°, then find :

(a) ∠BDA

(b) ∠BAD

(c) ∠CAD

(d) ∠ODB

(a) We know that,

Angle in a semi-circle is a right angle.

∴ ∠BDA = 90°.

Hence, ∠BDA = 90°.

(b) In △ BAD,

By angle sum property of triangle,

⇒ ∠BDA + ∠BAD + ∠ABD = 180°

⇒ 90° + ∠BAD + 26° = 180°

⇒ ∠BAD + 116° = 180°

⇒ ∠BAD = 180° - 116° = 64°.

Hence, ∠BAD = 64°.

(c) From figure,

CE is tangent to the circle.

Angle between tangent and radius of the circle is 90°.

From figure,

⇒ ∠CAD + ∠BAD = 90°

⇒ ∠CAD + 64° = 90°

⇒ ∠CAD = 90° - 64° = 26°.

Hence, ∠CAD = 26°.

(d) Join OD.

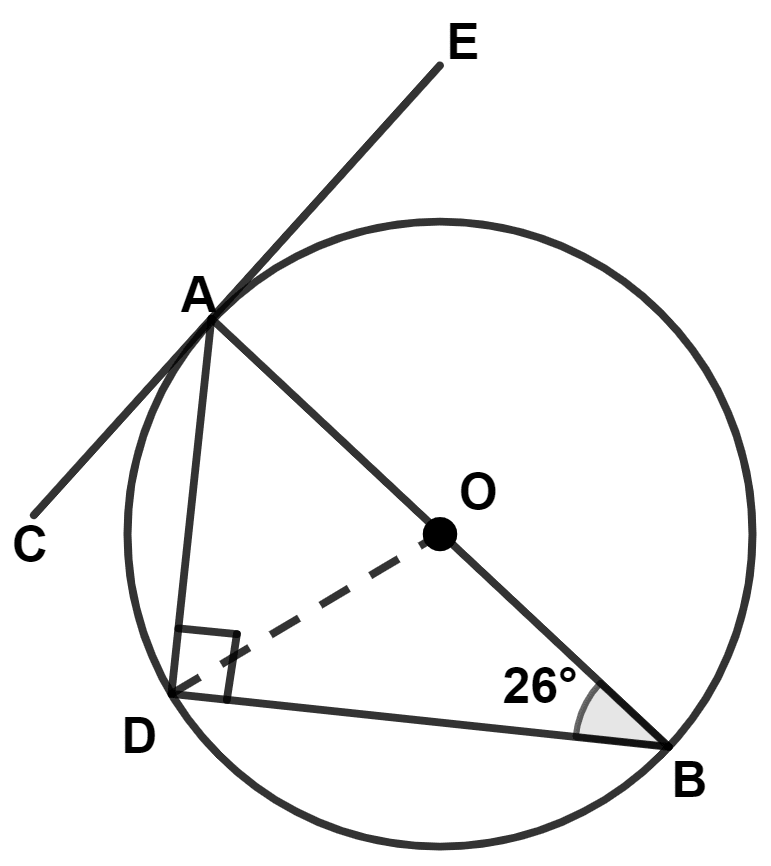
In △ OBD,

⇒ OD = OB (Radius of same circle)

We know that,

Angles opposite to equal sides are equal.

⇒ ∠ODB = ∠OBD = 26°.

Hence, ∠ODB = 26°.