Mathematics
Salman deposits ₹ 1,000 every month in a recurring deposit account for 2 years. If he receives ₹ 26,000 on maturity, find :
(a) total interest Salman earns
(b) the rate of interest.
Banking
ICSE 2023
39 Likes
Answer
(a) Given,
Salman deposits ₹ 1000 every month in a recurring deposit account for 2 years.
Total deposit = ₹ 1,000 × 2 × 12 = ₹ 24,000.
By formula,
Total interest earned = Maturity value - Total deposit
= ₹ 26,000 - ₹ 24,000
= ₹ 2,000.
Hence, interest earned = ₹ 2,000.
(b) Let rate of interest be r%. Time (n) = 24 months
By formula,
Interest =
Substituting values we get :
Hence, rate of interest earned = 8%.
Answered By
17 Likes
Related Questions
The solution set for the inequation 2x + 4 ≤ 14, x ∈ W is :
{1, 2, 3, 4, 5}
{0, 1, 2, 3, 4, 5}
{1, 2, 3, 4}
{0, 1, 2, 3, 4}
Find the value of 'a' if x - a is a factor of the polynomial 3x3 + x2 - ax - 81.
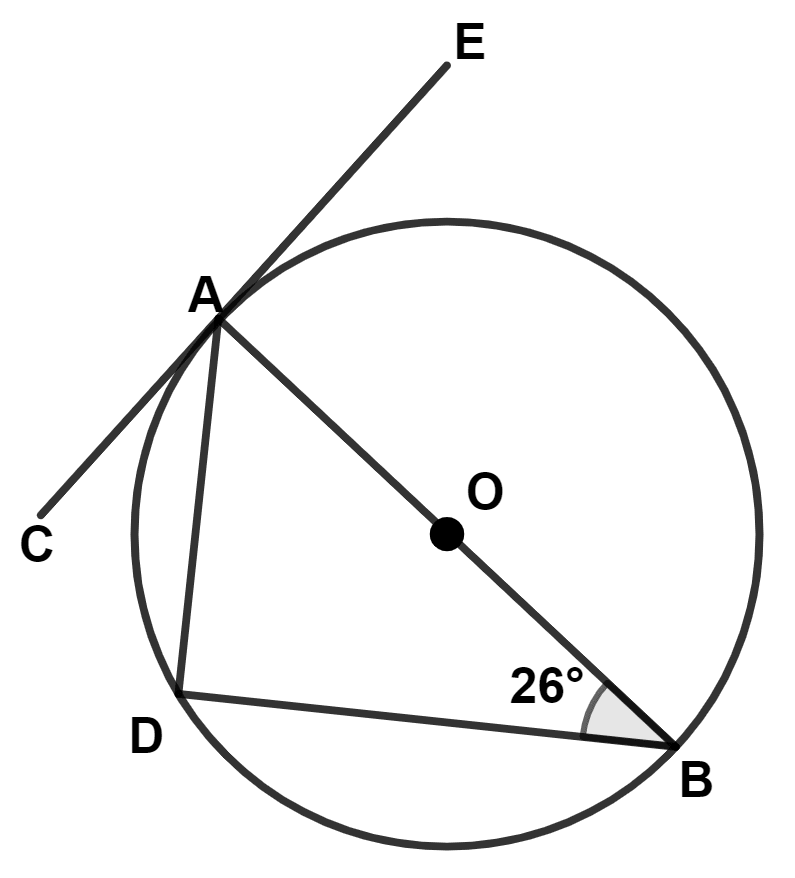
In the given figure O, is the center of the circle. CE is a tangent to the circle at A. If ∠ABD = 26°, then find :
(a) ∠BDA
(b) ∠BAD
(c) ∠CAD
(d) ∠ODB
Solve the following quadratic equation :
x2 + 4x - 8 = 0.
Give your answer correct to one decimal place.