Mathematics
Prove that the median drawn from the vertex P of an isosceles triangle △PQR with PQ = PR is perpendicular to QR and bisects ∠P.
Triangles
13 Likes
Answer
Let PQR be an isosceles triangle with PQ = PR.
Draw a median from vertex P to the side QR. Let this median be PS, where S is the midpoint of QR.
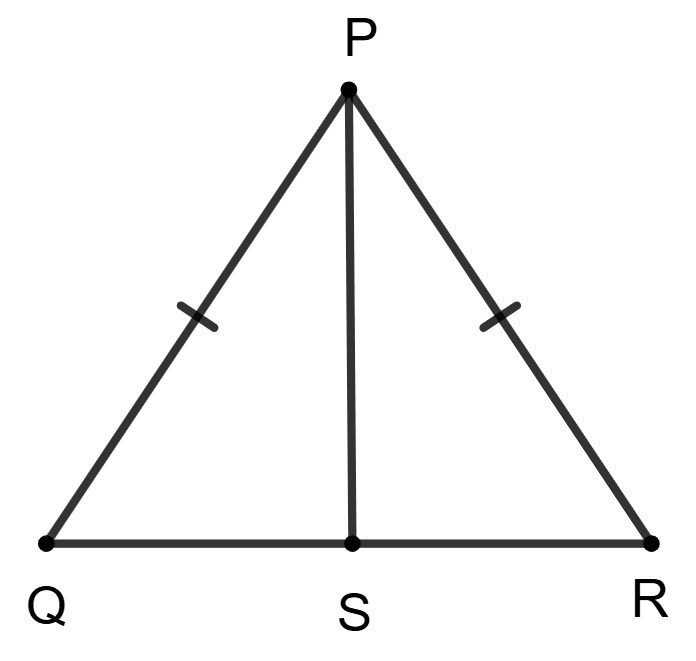
In △PQS and △PRS,
⇒ PQ = PR (△PQR is an isosceles triangle).
⇒ QS = RS (Since PS is the median, S is the midpoint of QR).
⇒ PS = PS (Common side to both triangles).
By the SSS (Side-Side-Side) congruence criterion,
△PQS ≅ △PRS
We know that,
Corresponding parts of congruent triangles are congruent.
⇒ ∠PSQ = ∠PSR = x (let)
From figure,
⇒ ∠PSQ + ∠PSR = 180° [Linear pair]
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = = 90°.
⇒ ∠PSQ = ∠PSR = 90°.
Thus, PS is perpendicular to QR.
So, PS ⊥ QR.
⇒ ∠QPS = ∠RPS (By C.P.C.T.C.)
Thus, PS bisects ∠P.
Hence, the median drawn from the vertex P of an isosceles triangle △PQR is perpendicular to QR and bisects ∠P.
Answered By
8 Likes
Related Questions
In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) △ACE ≅ △DBF
(ii) AE = DF.

Two line segments AC and BD bisect each other at P. Draw the diagram and prove that
(i) AB = CD
(ii) ∠BAC = ∠DCA
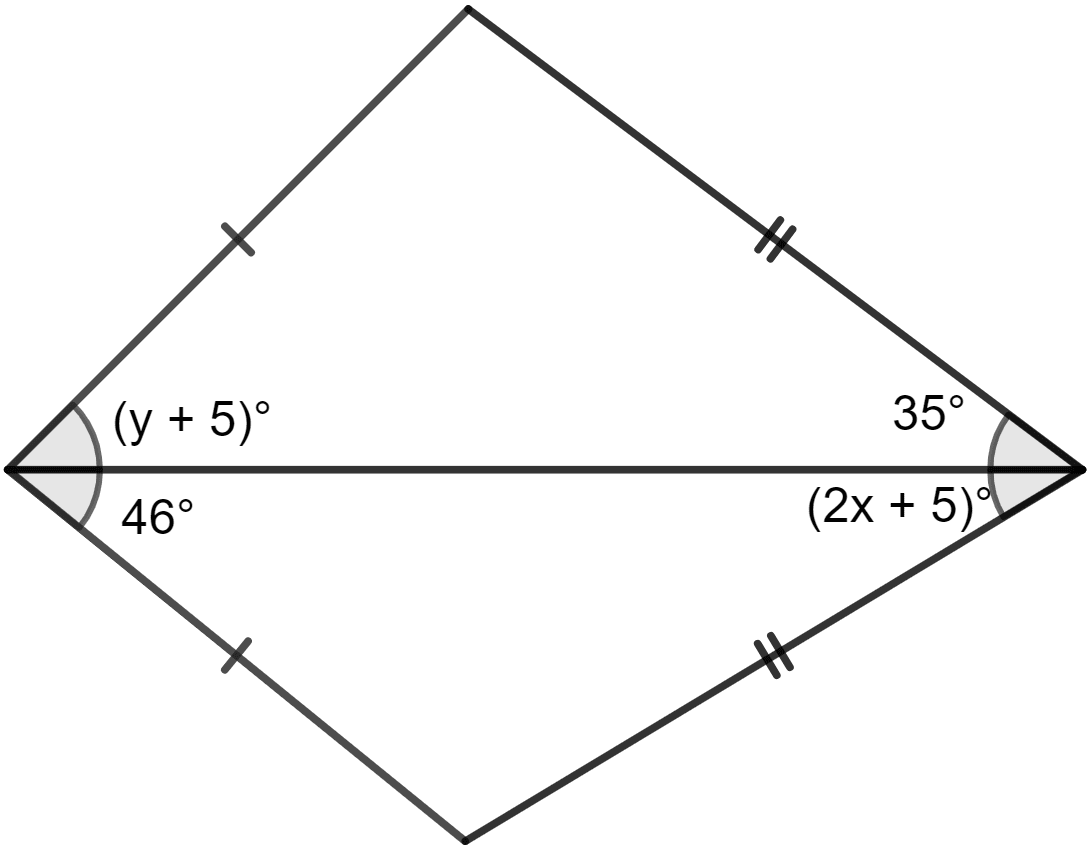
In the adjoining figure, find the values of x and y.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of △PQR should be equal to side AB of △ABC so that the two triangles are congruent? Give reason for your answer.