Mathematics
Two line segments AC and BD bisect each other at P. Draw the diagram and prove that
(i) AB = CD
(ii) ∠BAC = ∠DCA
Triangles
17 Likes
Answer
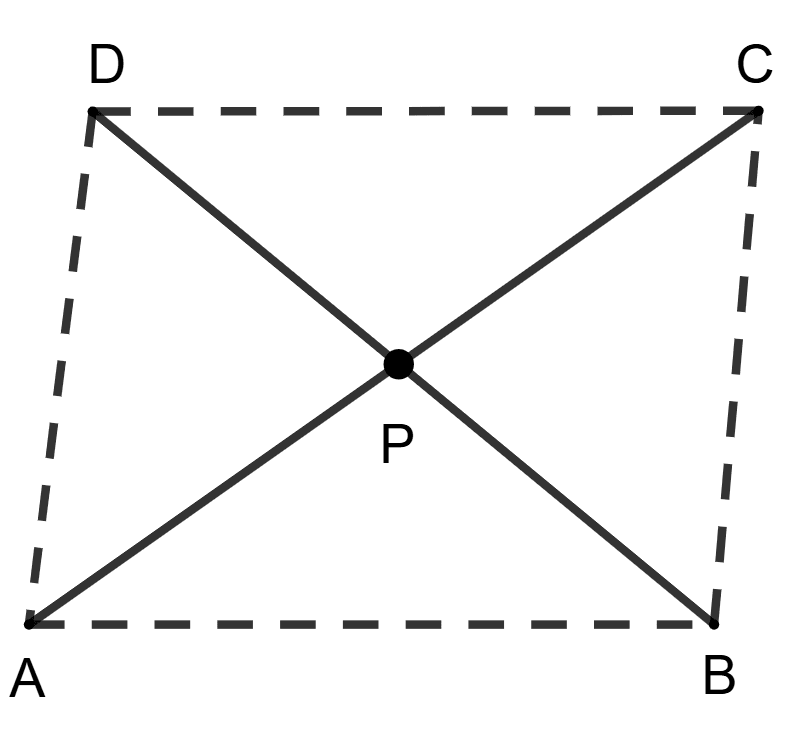
(i) Given, AC and BD bisect each other at P.
Join CD, BC, AB and AD.
In △BPA and △CPD,
As, P bisects AC and BD
⇒ PA = PC (P bisects AC and BD)
⇒ PB = PD (P bisects AC and BD)
⇒ ∠BPA = ∠CPD (Vertically opposite angles are equal).
∴ △BPA ≅ △CPD by SAS axiom.
We know that corresponding sides of congruent triangles are equal.
∴ AB = CD (By C.P.C.T.C.)
Hence, proved that AB = CD.
(ii) As proved in part (i),
△BPA ≅ △CPD by SAS axiom.
We know that corresponding angles of congruent triangles are equal.
∠DCP = ∠PAB ……………………(1)
From figure we get,
∠DCP = ∠DCA and ∠PAB = ∠BAC.
Substituting above values in equation (1) we get,
∠DCA = ∠BAC.
Hence, proved that ∠BAC = ∠DCA.
Answered By
7 Likes
Related Questions
In the adjoining figure, AB = AC and D is the midpoint of BC. Use SSS rule of congruency to show that
(i) △ABD ≅ △ACD
(ii) AD is bisector of ∠A
(iii) AD is perpendicular to BC.

In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) △ACE ≅ △DBF
(ii) AE = DF.

Prove that the median drawn from the vertex P of an isosceles triangle △PQR with PQ = PR is perpendicular to QR and bisects ∠P.
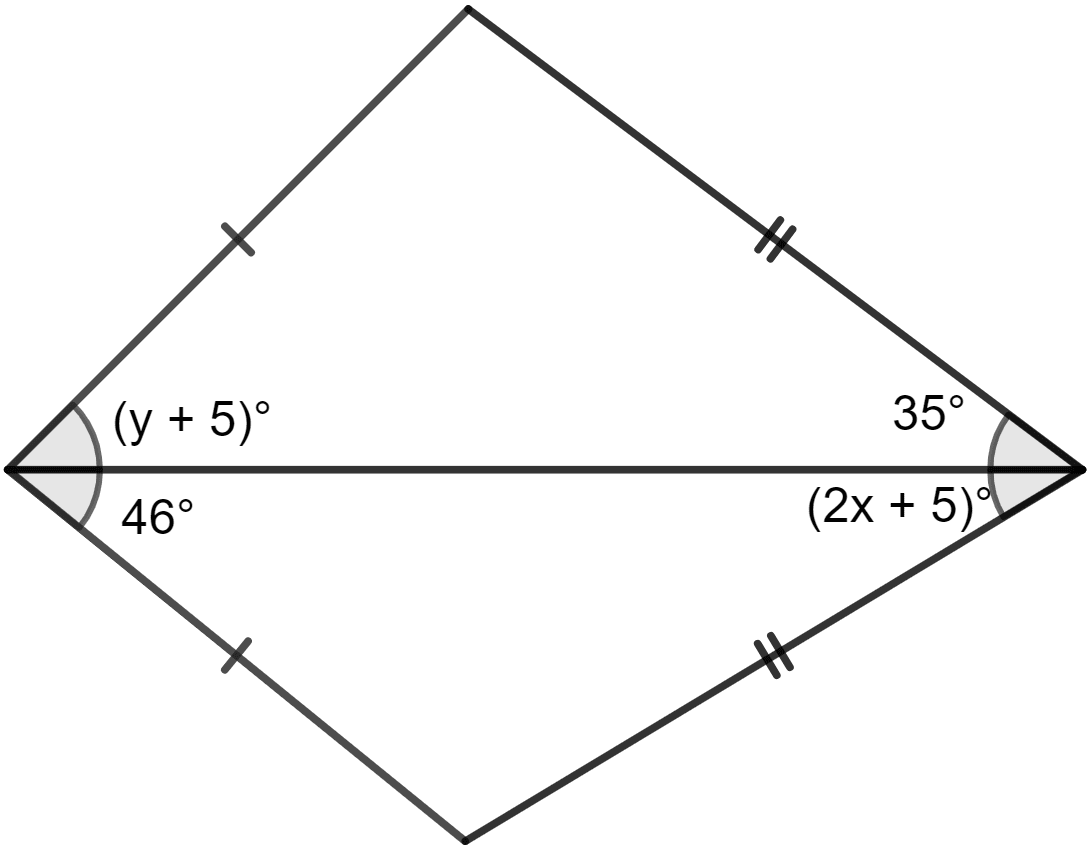
In the adjoining figure, find the values of x and y.