Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

We know that,

The circles are congruent, their radii will be equal.

Let, there be two circles with center P and X with equal radius.

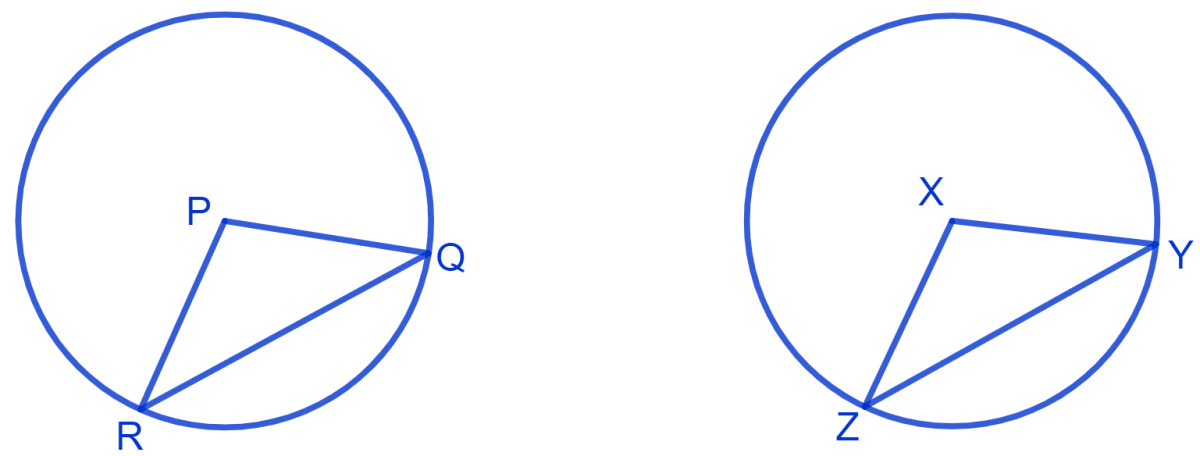
Since,

Chords of congruent circles subtend equal angles at their centres

∴ ∠QPR = ∠YXZ.

⇒ PR = PQ = XZ = XY

In ∆ PQR and ∆ XYZ,

⇒ PQ = XY (Radius of congruent circles are equal)

⇒ ∠QPR = ∠YXZ (Chords subtend equal angles at center)

⇒ PR = XZ (Radius of congruent circles are equal)

∴ ∆ PQR ≅ ∆ XYZ. (By S.A.S. congruence rule)

We know that,

Corresponding parts of congruent triangles are equal.

∴ QR = YZ (By C.P.C.T.)

Hence, proved that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.