Mathematics
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
Mid-point Theorem
45 Likes
Answer
Let ABCD be the rectangle and P, Q, R and S be the mid-points of sides AB, BC, CD and DA respectively. Join PQRS.
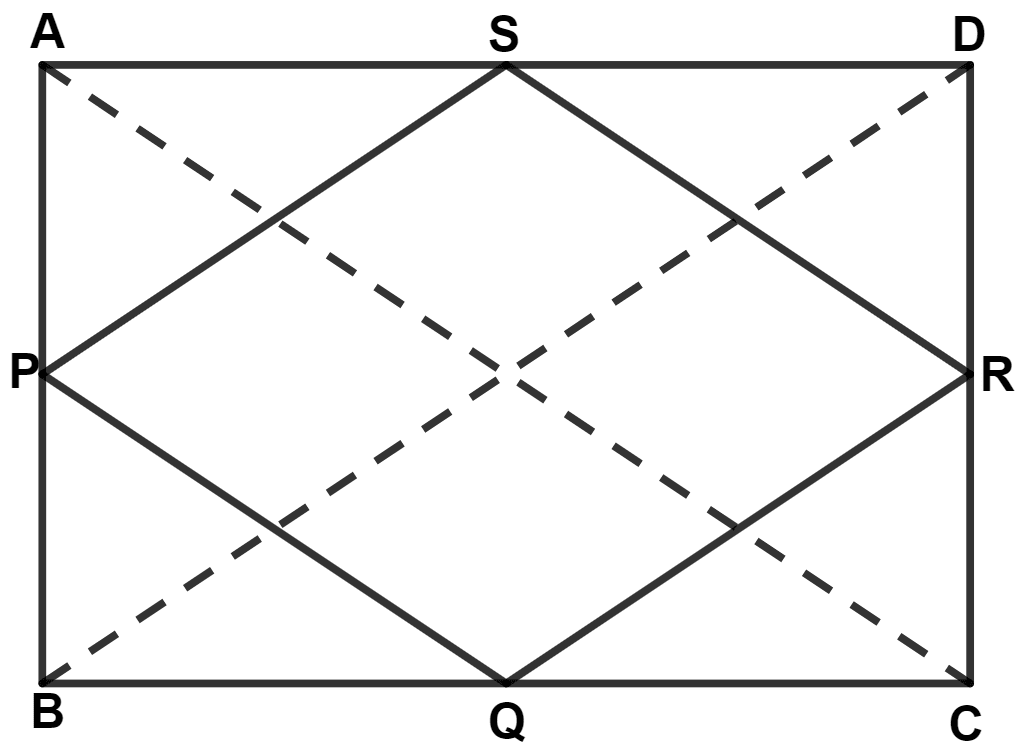
By mid-point theorem,
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
Join AC and BD.
We know that,
Diagonals of a rectangle are equal.
∴ AC = BD = x (let)
In Δ ABC, P and Q are the mid-points of sides AB and BC respectively.
∴ PQ || AC and PQ = (By mid-point theorem) ……..(1)
In Δ ADC, S and R are mid-points of sides AD and CD respectively.
∴ SR || AC and SR = (By mid-point theorem) ………(2)
From equations (1) and (2), we get :
PQ || SR and PQ = SR
In Δ ABD, P and S are the mid-points of sides AB and AD respectively.
∴ PS || BD and PS = (By mid-point theorem) ……..(3)
In Δ BDC, Q and R are mid-points of sides BC and CD respectively.
∴ QR || BD and QR = (By mid-point theorem) ………(4)
From equations (3) and (4), we get :
PQ || SR and PS = QR
By using equation (1), (2), (3) and (4), we get :
⇒ PQ = QR = SR = PS
Since, opposite sides are parallel and all the sides are equal.
∴ PQRS is a rhombus.
Hence, proved that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
Answered By
25 Likes
Related Questions
P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively of rectangle ABCD, then quadrilateral PQRS is :
rectangle
rhombus
square
parallelogram
In triangle ABC, M is the mid-point of AB and a straight line through M and parallel to BC cuts AC at N. Find the lengths of AN and MN, if BC = 7 cm and AC = 5 cm.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles △ ABC in which AB = BC. Prove that △ DEF is also isosceles.
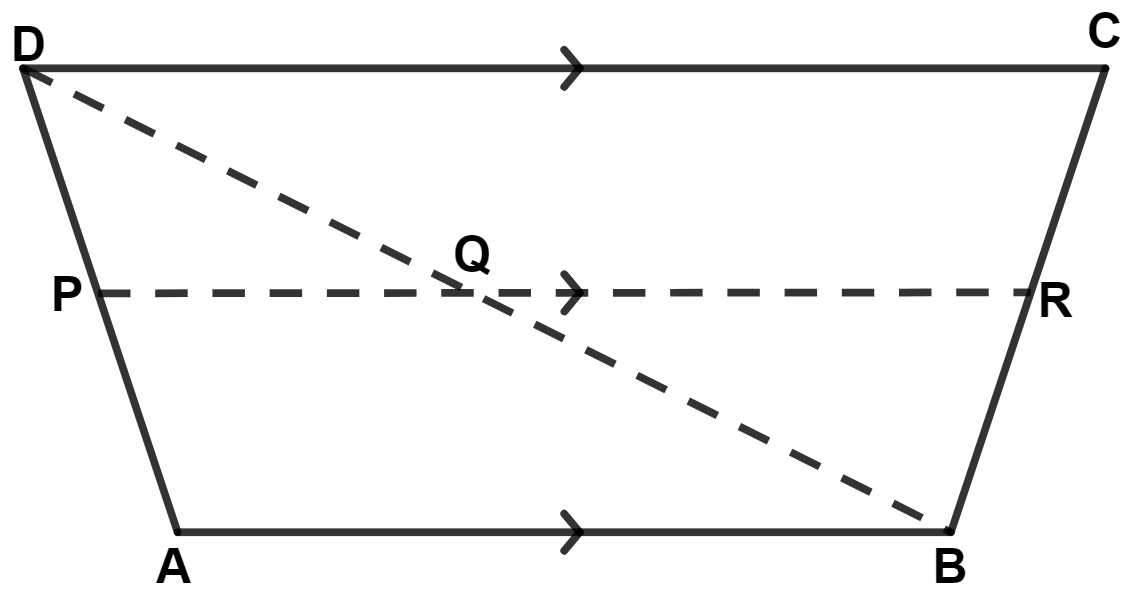
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that :
PR = (AB + CD)