Mathematics
In quadrilateral ABCD, AB = AD and CB = CD. Prove that AC is perpendicular bisector of BD.
Triangles
7 Likes
Answer
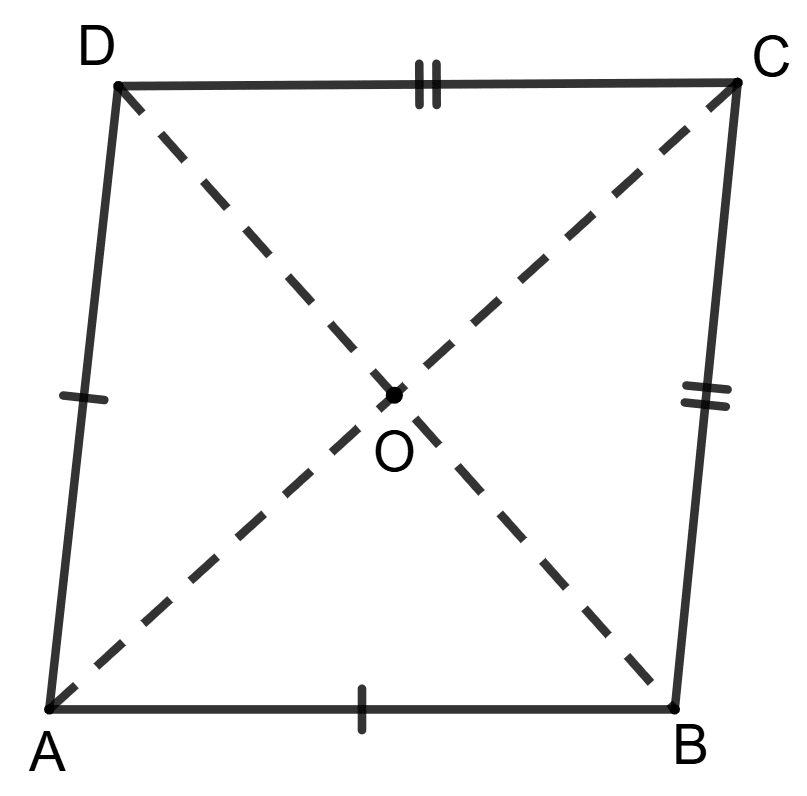
In △ ABC and △ ADC,
⇒ AB = AD (Given)
⇒ BC = CD (Given)
⇒ AC = AC (Common side)
∴ △ ABC ≅ △ ADC (By S.S.S. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ ∠BAC = ∠DAC
⇒ ∠BAO = ∠DAO
In △ AOB and △ AOD,
⇒ AB = AD (Given)
⇒ AO = AO (Common side)
⇒ ∠BAO = ∠DAO (Proved above)
∴ △ AOB ≅ △ AOD (By S.A.S. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ ∠BOA = ∠DOA …….(1)
⇒ OB = OD
From figure,
⇒ ∠BOA + ∠DOA = 180° (Linear pair)
⇒ ∠BOA + ∠BOA = 180° [From equation (1)]
⇒ 2∠BOA = 180°
⇒ ∠BOA = = 90°.
∴ AC is perpendicular bisector of BD.
Hence, proved that AC is perpendicular bisector of BD.
Answered By
6 Likes
Related Questions
Assertion (A): ΔABD ≅ ΔACE
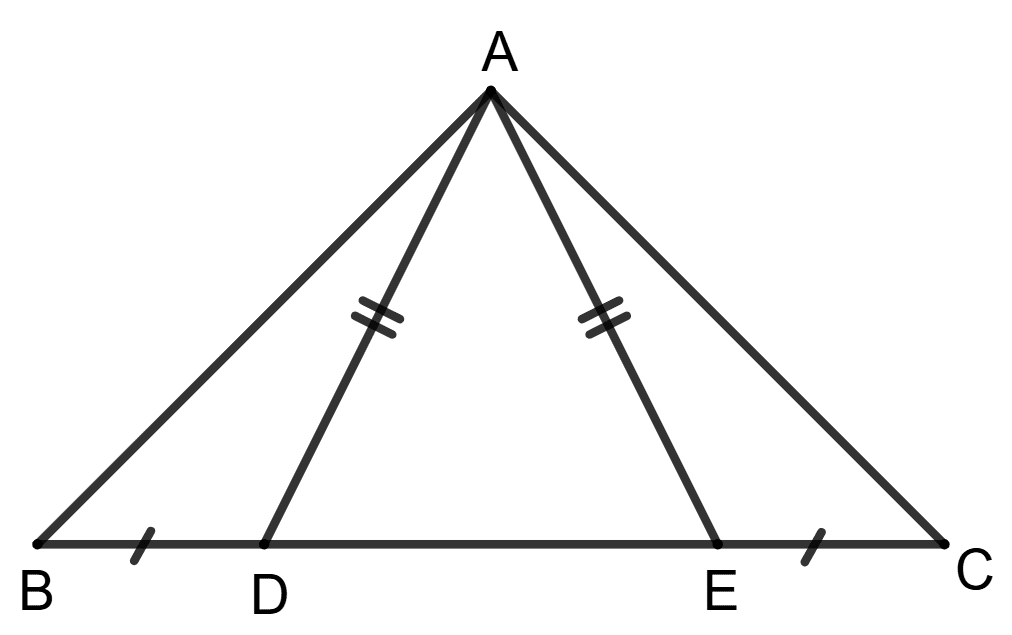
Reason (R): ∠ADE + ∠ADB = ∠AEC + ∠AED
But AD = AE
⇒ ∠ADE = ∠AED
∴ ∠ADB = ∠AEC
⇒ ∠ABD ≅ ∠AEC
A is true, but R is false.
A is false, but R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.
Which of the following pairs of triangles are congruent ? In each case, state the condition of congruency :
(a) In △ ABC and △ DEF, AB = DE, BC = EF and ∠B = ∠E.
(b) In △ ABC and △ DEF, ∠B = ∠E = 90°; AC = DF and BC = EF.
(c) In △ ABC and △ QRP, AB = QR, ∠B = ∠R and ∠C = ∠P.
(d) In △ ABC and △ PQR, AB = PQ, AC = PR and BC = QR.
(e) In △ ABC and △ PQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
In the given figure : AB // FD, AC // GE and BD = CE; prove that :
(i) BG = DF
(ii) CF = EG.
In a triangle ABC, AB = AC. Show that the altitude AD is median also.