Mathematics
Represent the following inequalities on real number lines :
(i) 2x - 1 < 5
(ii) 3x + 1 ≥ -5
(iii) 2(2x - 3) ≤ 6
(iv) -4 < x < 4
(v) -2 ≤ x < 5
(vi) 8 ≥ x > -3
(vii) -5 < x ≤ -1
Linear Inequations
46 Likes
Answer
(i) 2x - 1 < 5
⇒ 2x < 5 + 1
⇒ 2x < 6
⇒ x < 3
Solution on the number line is :

(ii) 3x + 1 ≥ -5
⇒ 3x ≥ -5 - 1
⇒ 3x ≥ -6
Dividing both sides by 3 we get,
⇒ x ≥ -2
Solution on the number line is :
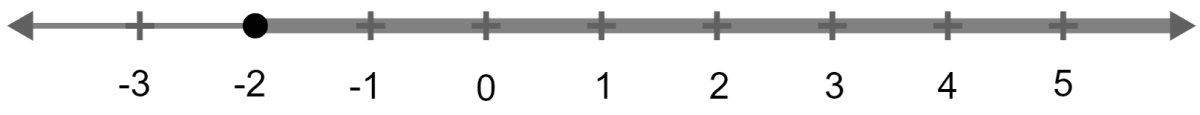
(iii) 2(2x - 3) ≤ 6
⇒ 4x - 6 ≤ 6
⇒ 4x ≤ 6 + 6
⇒ 4x ≤ 12
Dividing both sides by 4 we get,
⇒ x ≤ 3
Solution on the number line is :

(iv) -4 < x < 4
Solution on the number line is :

(v) -2 ≤ x < 5
Solution on the number line is :

(vi) 8 ≥ x > -3
Solution on the number line is :

(vii) -5 < x ≤ -1
Solution on the number line is :

Answered By
34 Likes
Related Questions
The solution set for the following number line is :
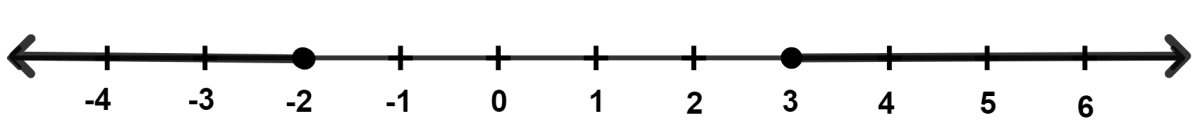
{x : x ∈ R, x < -2 and x > 3}
{x : x ∈ R and -2 < x < 3}
{x : x ∈ R, x < -2 or x < 3}
{x : x ∈ R, x ≤ -2 or x ≥ 3}
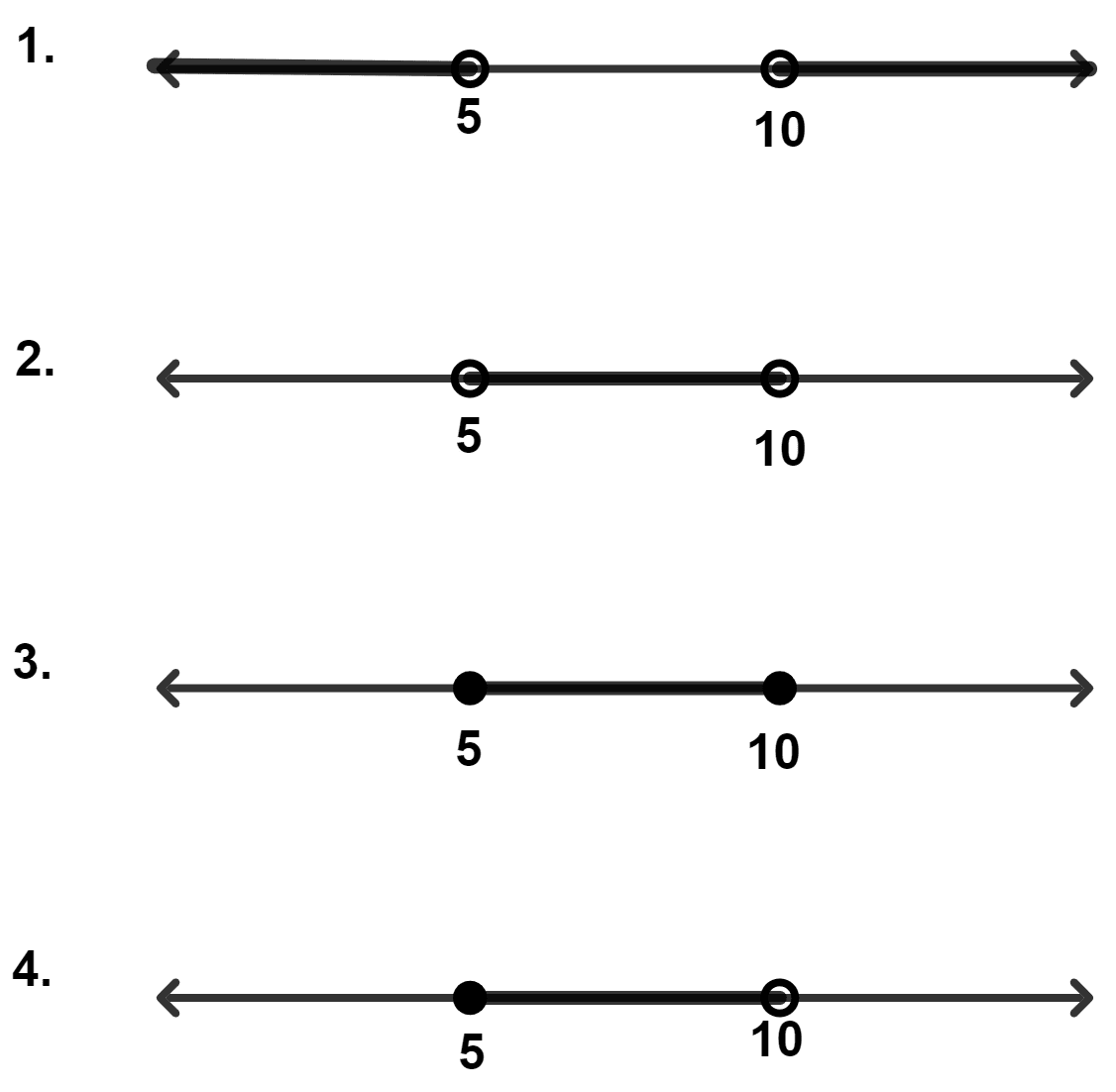
The number line for the solution of inequation x > 5 and x < 10 (x ∈ R) is :
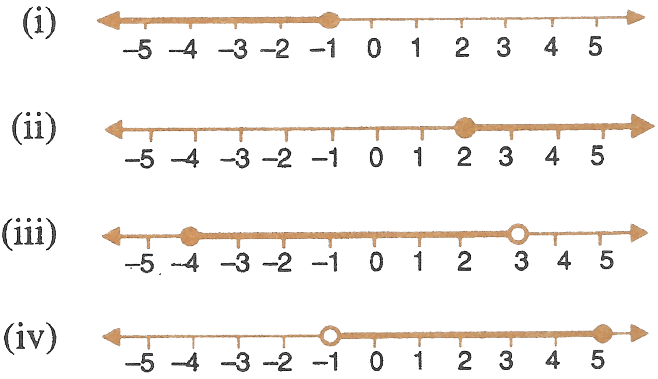
For each graph given alongside, write an inequation taking x as the variable :
For the following inequations, graph the solution set on the real number line :
-4 ≤ 3x - 1 < 8