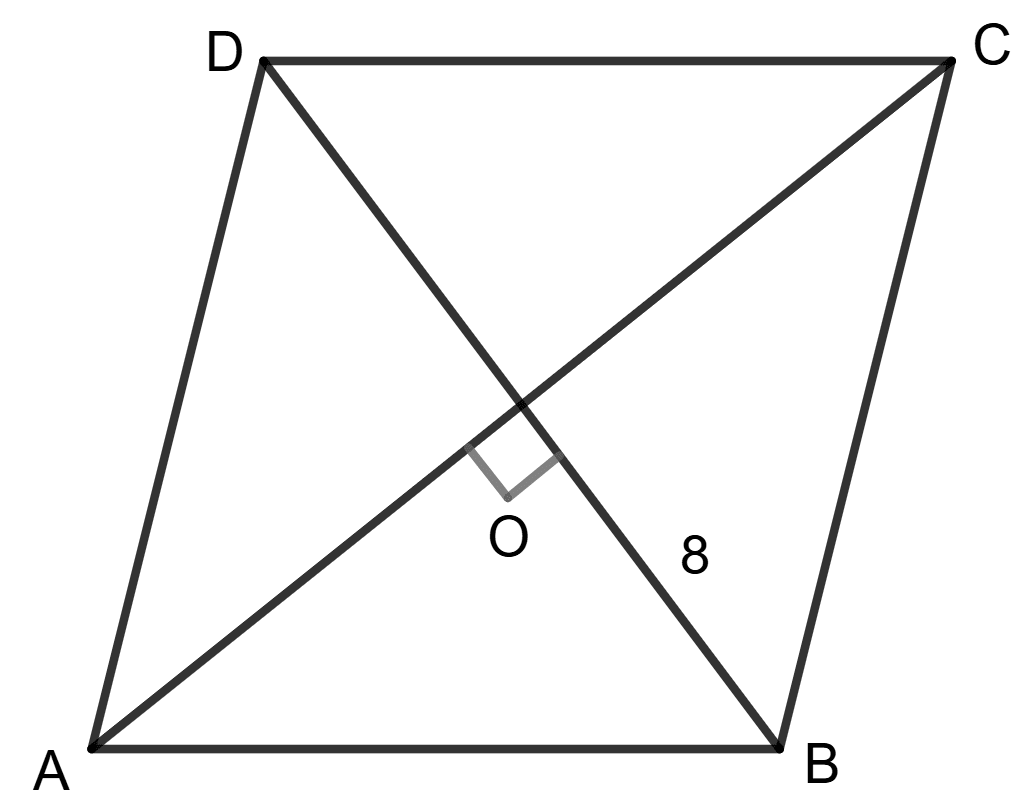
In rhombus ABCD, diagonals AC and BD intersect each other at point O.

If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.

As we know that the diagonals of a rhombus bisect each other at right angles.

cos ∠CAB = 0.6 = $\dfrac{6}{10} = \dfrac{3}{5}$

cos ∠CAB = $\dfrac{Base}{Hypotenuse} = \dfrac{3}{5}$

∴ If length of OA = 3x cm, length of AB = 5x cm.

In Δ ABO,

⇒ AB² = AO² + BO² (∵ AB is hypotenuse)

⇒ (5x)² = (3x)² + BO²

⇒ 25x² = 9x² + BO²

⇒ BO² = 25x² - 9x²

⇒ BO² = 16x²

⇒ BO = $\sqrt{16\text{x}^2}$

⇒ BO = 4x

It is given that OB = 8 cm

So, 4x = 8

x = $\dfrac{8}{4} = 2$

Therefore, OA = 3x = 3 x 2 = 6 cm and AB = 5x = 5 x 2 cm = 10 cm.

Diagonal BD = 2 x OB = 2 x 8 cm = 16 cm

Diagonal AC = 2 x OA = 2 x 6 cm = 12 cm

Hence, diagonals = 16 cm and 12 cm and side = 10 cm.