Mathematics
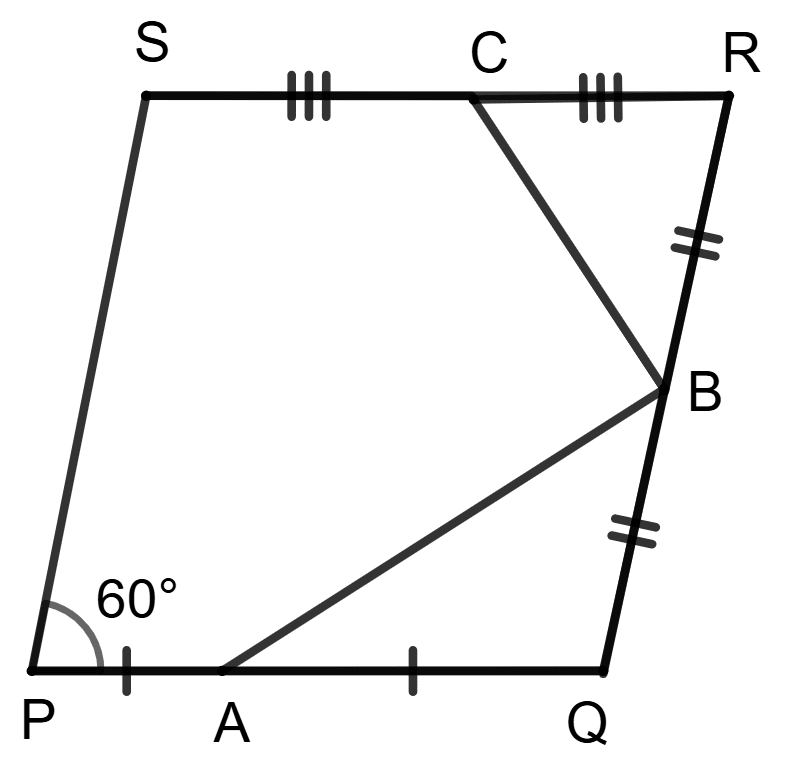
In rhombus PQRS; A, B and C are mid-points of sides PQ, QR and RS respectively. If ∠P = 60°, the angle PQR is equal to:
60°
90°
120°
none of these
Mid-point Theorem
3 Likes
Answer
Given, ∠P = 60°
∠P and ∠PQR are consecutive angles in the rhombus.
The sum of consecutive angles in a rhombus is 180°.
⇒ ∠P + ∠PQR = 180°
⇒ 60° + ∠PQR = 180°
⇒ ∠PQR = 180° - 60°
⇒ ∠PQR = 120°.
Hence, option 3 is the correct option.
Answered By
1 Like
Related Questions
In the given figure, AB || CD || EF. If AC = 7 cm, AE = 14 cm and BF = 20 cm, then DF is equal to:
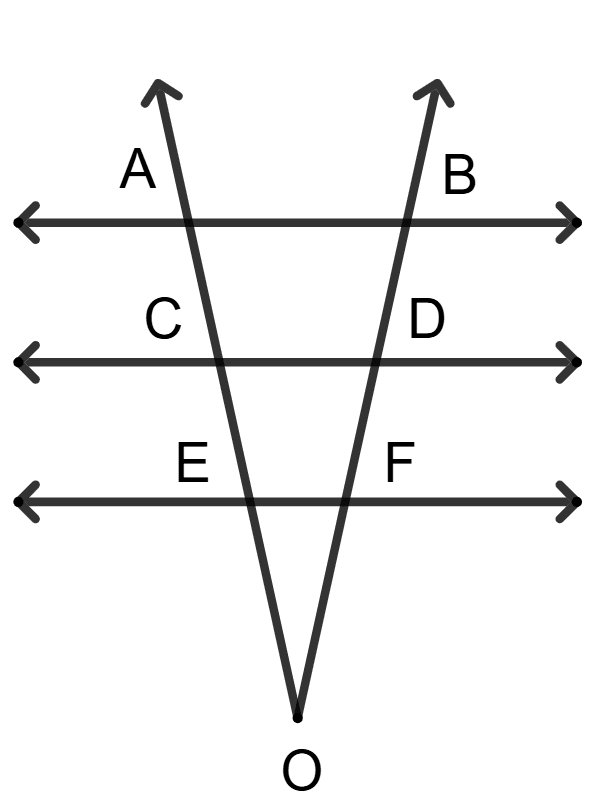
7 cm
14 cm
10 cm
16 cm
In the given figure, AB || CD || EF and E is the mid-point of side AD, then :
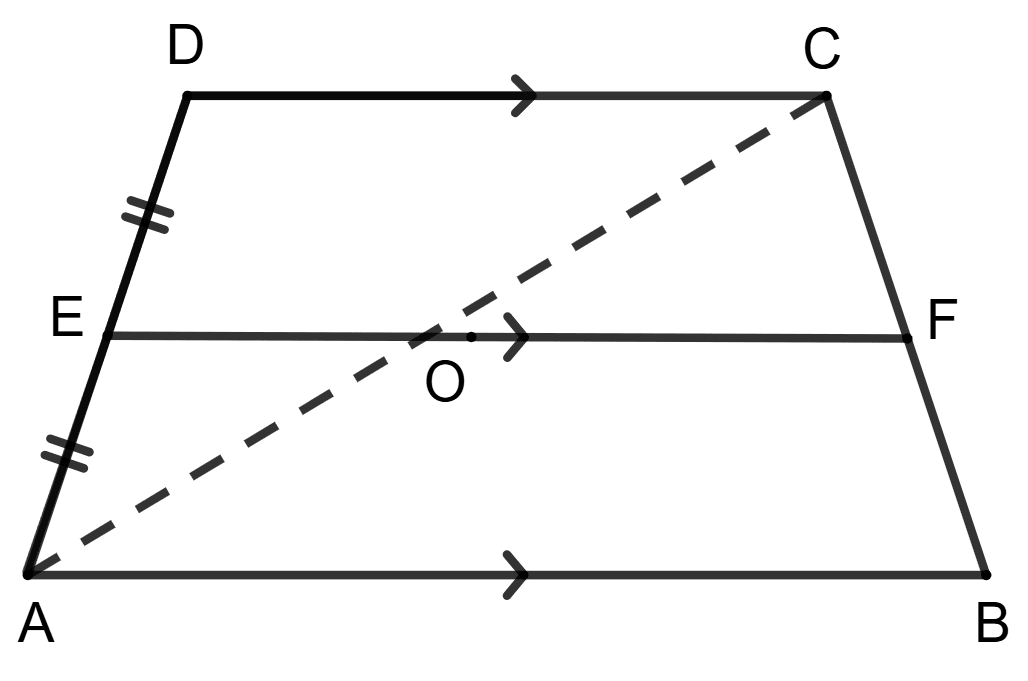
OE : OF = 1 : 3
OE = OF
OF = 2 x OE
CF = FB
Statement 1: The diagonals of a quadrilateral are perpendicular to each other; P, Q, R and S are the midpoints of sides AB, BC, CD and DA respectively.
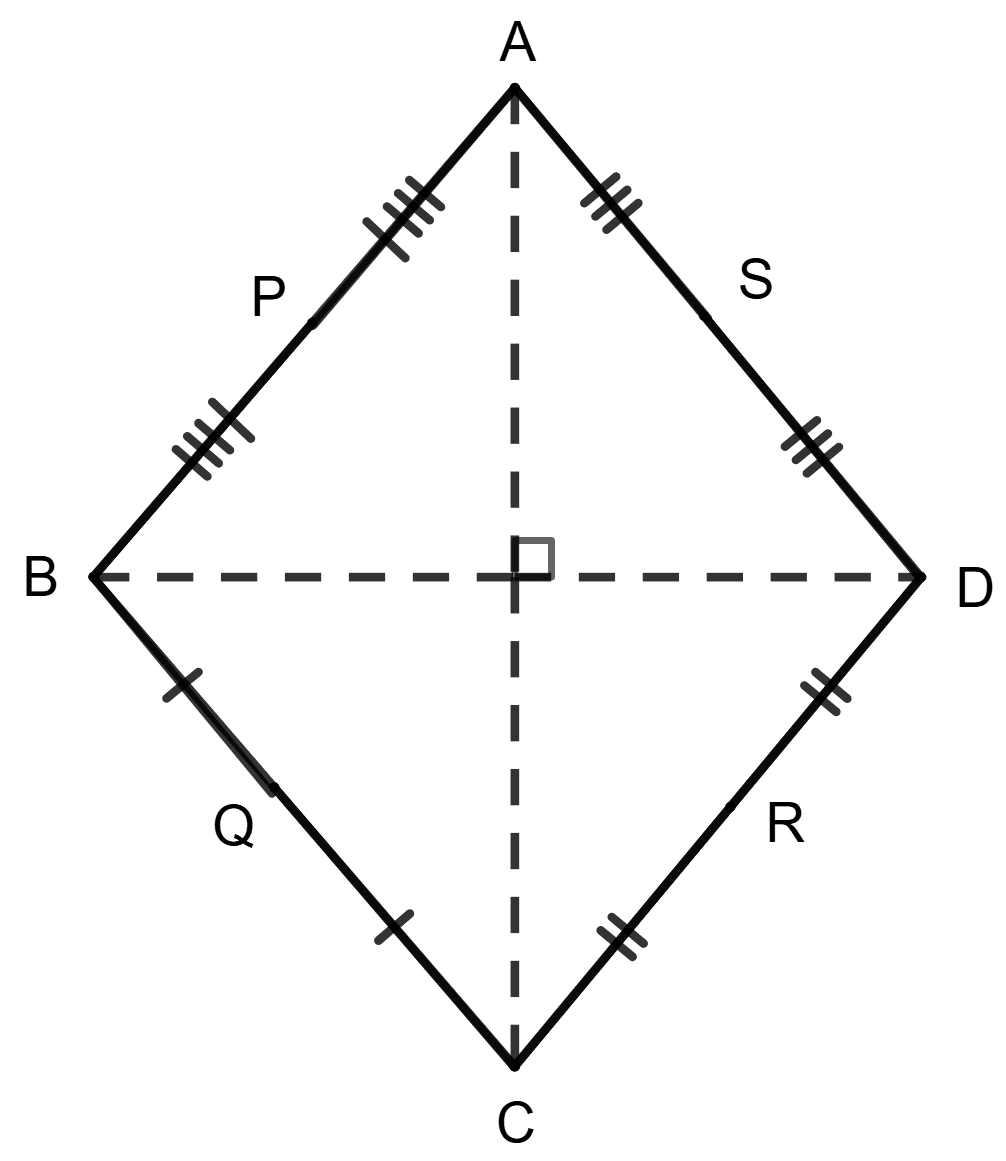
Statement 2: Quadrilateral PQRS is a square.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: AD is median of triangle ABC and DE is parallel to BA.
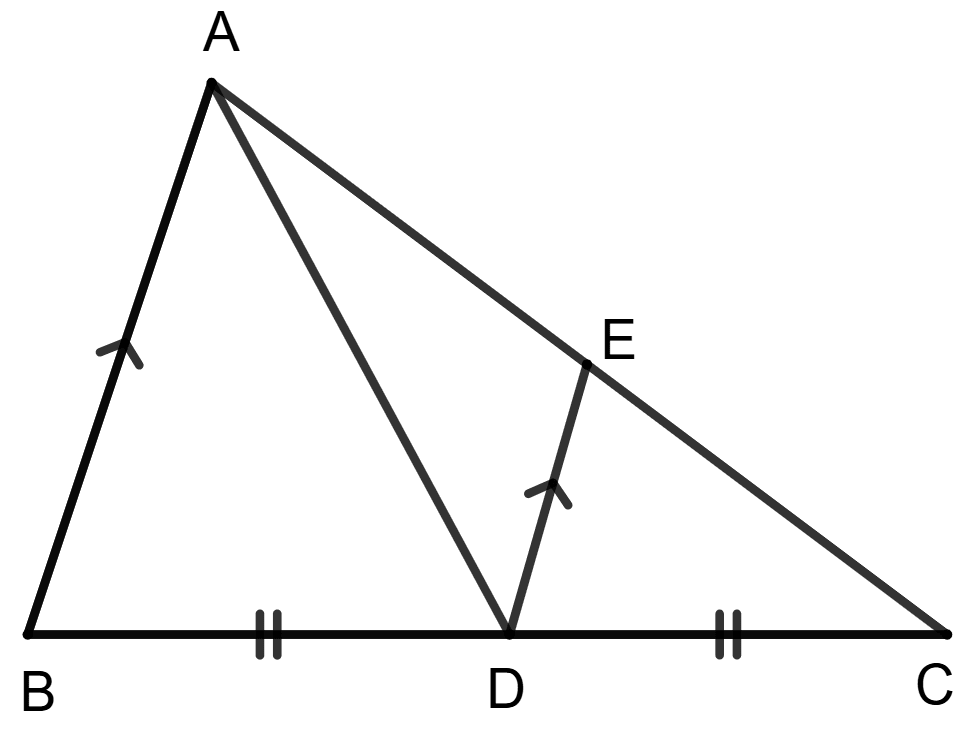
Statement 2: DE is median of triangle ADC.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.