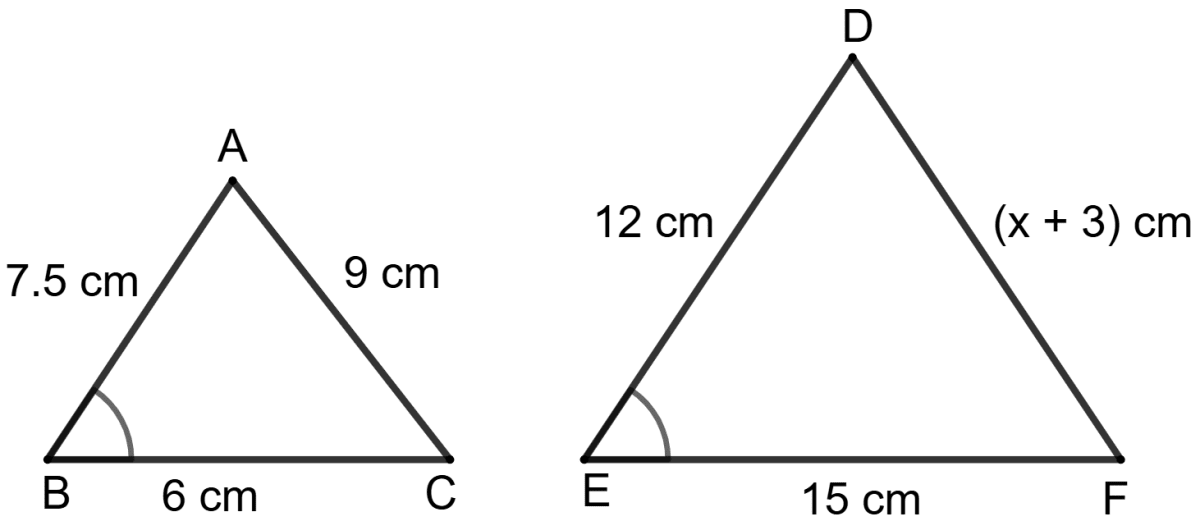
Mathematics
Sides AB, BC and median AD of the triangle ABC are respectively proportional to sides PQ, QR and median PM of triangle PQR.
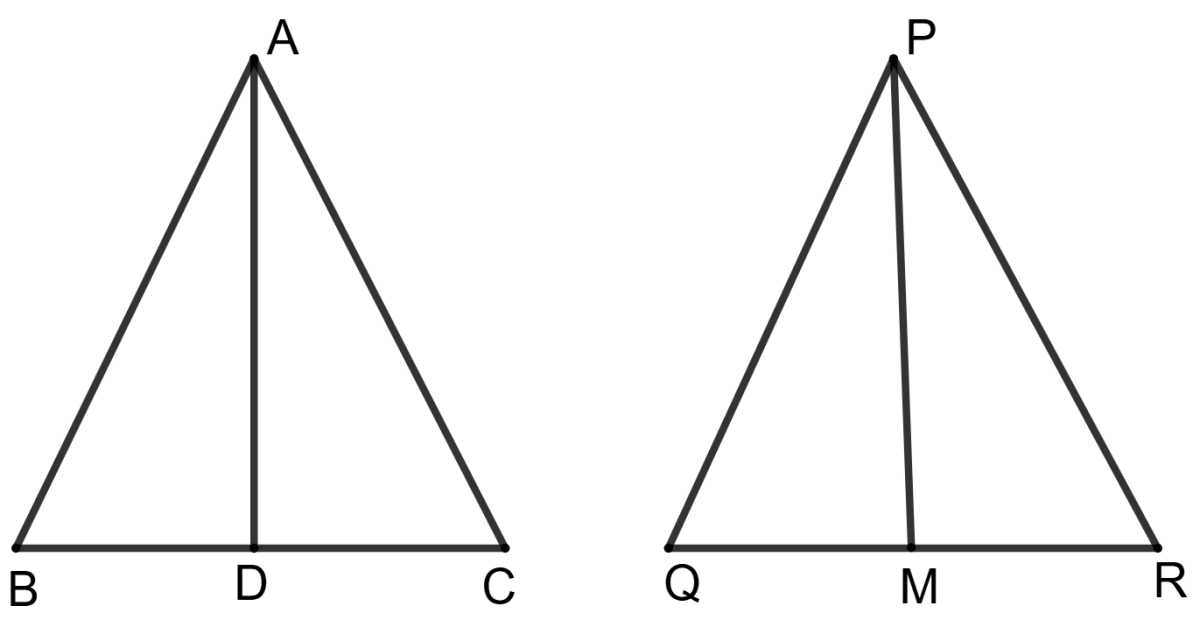
Prove that:
(i) Δ ABD ∼ Δ PQM
(ii) Δ ABC ∼ Δ PQR
Similarity
27 Likes
Answer
(i) Given, AB, BC and median AD of the triangle ABC are respectively proportional to sides PQ, QR and median PM of triangle PQR.
AD is median of triangle ABC.
∴ BD = DC = BC
PM is median of triangle PQR.
∴ QM = RM = QR
In Δ ABD and Δ PQM,
∴ Δ ABD ∼ Δ PQM (By SSS postulates)
Hence, Δ ABD ∼ Δ PQM.
(ii) From (i), Δ ABD ∼ Δ PQM
Corresponding angles of similar triangles are equal.
∴ ∠ABD = ∠PQM …………….(1)
In Δ ABC and Δ PQR,
⇒ ∠ABC = ∠PQR [From equation (1)]
∴ Δ ABC ∼ Δ PQR (By SAS postulate)
Hence, Δ ABC ∼ Δ PQR.
Answered By
19 Likes