Mathematics
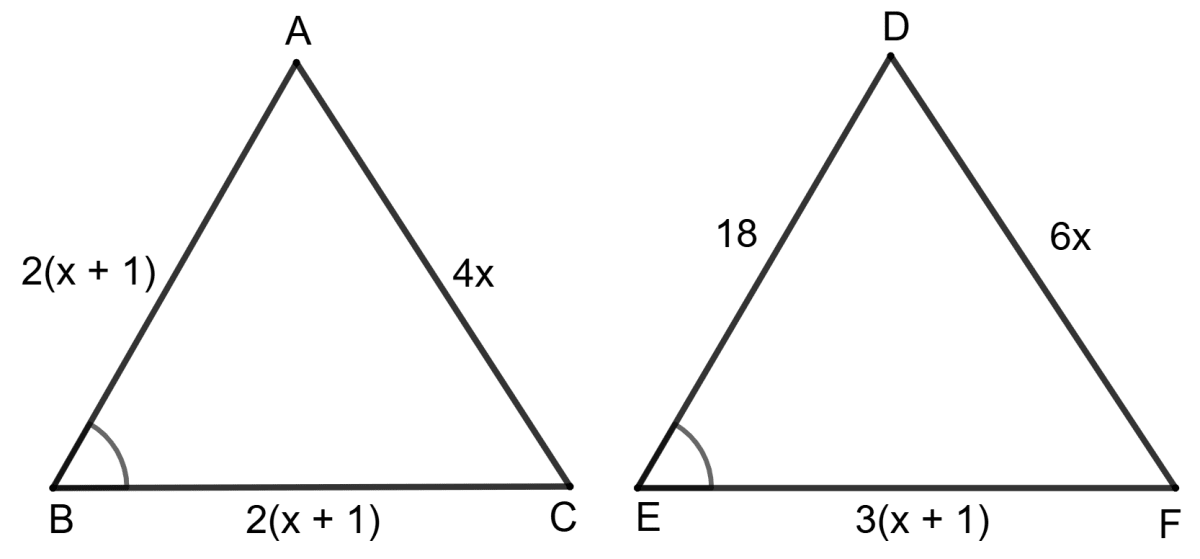
In the given figure, Δ ABC ∼ Δ DEF. Find the lengths of the sides of both the triangles (Each side is in cm).
Similarity
31 Likes
Answer
Given, Δ ABC ∼ Δ DEF
We know that,
Corresponding sides of similar triangles are proportional.
Now, in Δ ABC, AB = 2x + 1 = 2 × + 1 = 11 + 1 = 12 cm
BC = 2(x + 1) = cm
AC = 4x = 4 × = 22 cm
Now, in Δ DEF, DE = 18 cm
EF = 3(x + 1) = cm
DF = 6x = 6 × = 33 cm
Hence, AB = 12 cm, BC = 13 cm, AC = 22 cm, DE = 18 cm, EF = cm and DF = 33 cm.
Answered By
20 Likes
Related Questions
Sides AB, BC and median AD of the triangle ABC are respectively proportional to sides PQ, QR and median PM of triangle PQR.
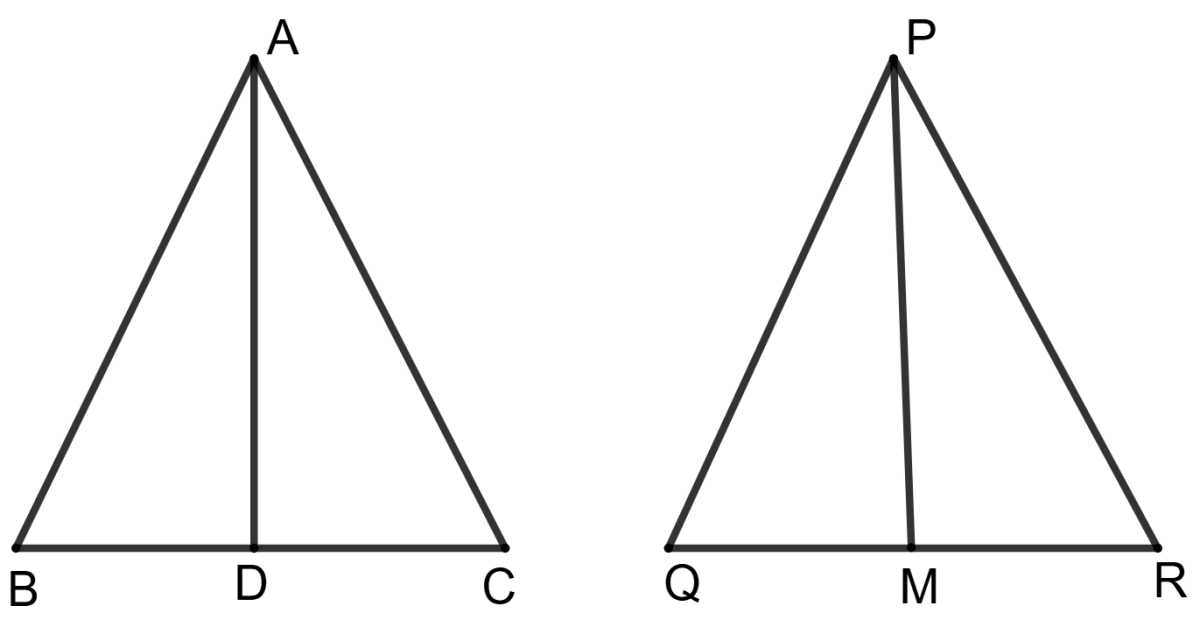
Prove that:
(i) Δ ABD ∼ Δ PQM
(ii) Δ ABC ∼ Δ PQR
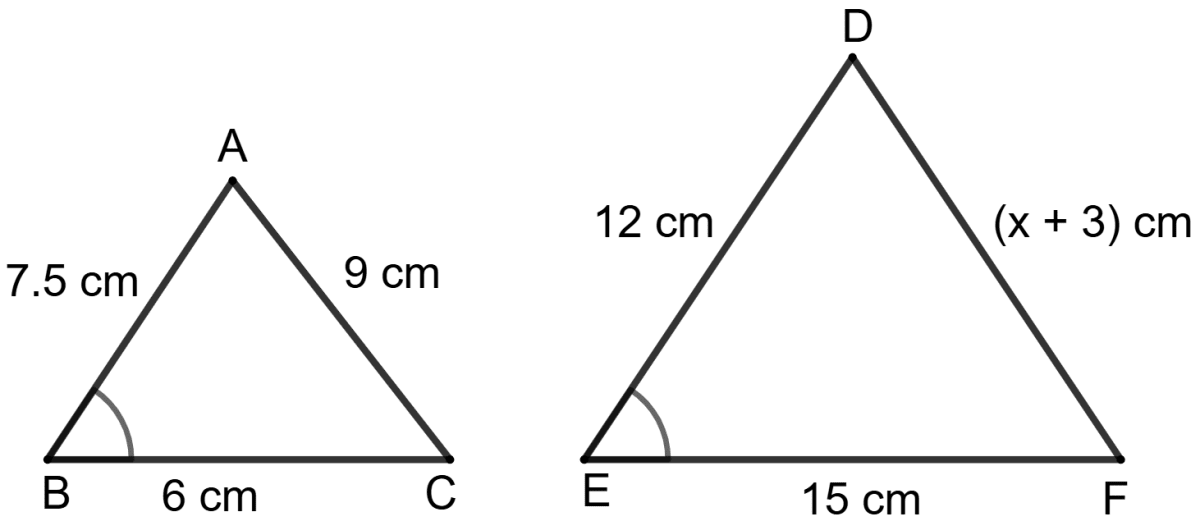
Find the value of x, if ∠B = ∠E.
In Δ ABC and Δ DEF, AB = 3 x DF, BC = 3 x DE and AC = 3 x EF. Show that the given triangle are similar. Name the two similar triangle on a proper way.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:
(i) ΔAPB is similar to ΔCPD.
(ii) PA x PD = PB x PC.