Mathematics
Solve, graphically, the following pairs of equations :
(i)
x - 5 = 0
y + 4 = 0
(ii)
2x + y = 23
4x - y = 19
(iii)
3x + 7y = 27
(iv)
Graphical Solution
24 Likes
Answer
(i) x - 5 = 0
⇒ x = 5
and, y + 4 = 0
⇒ y = - 4
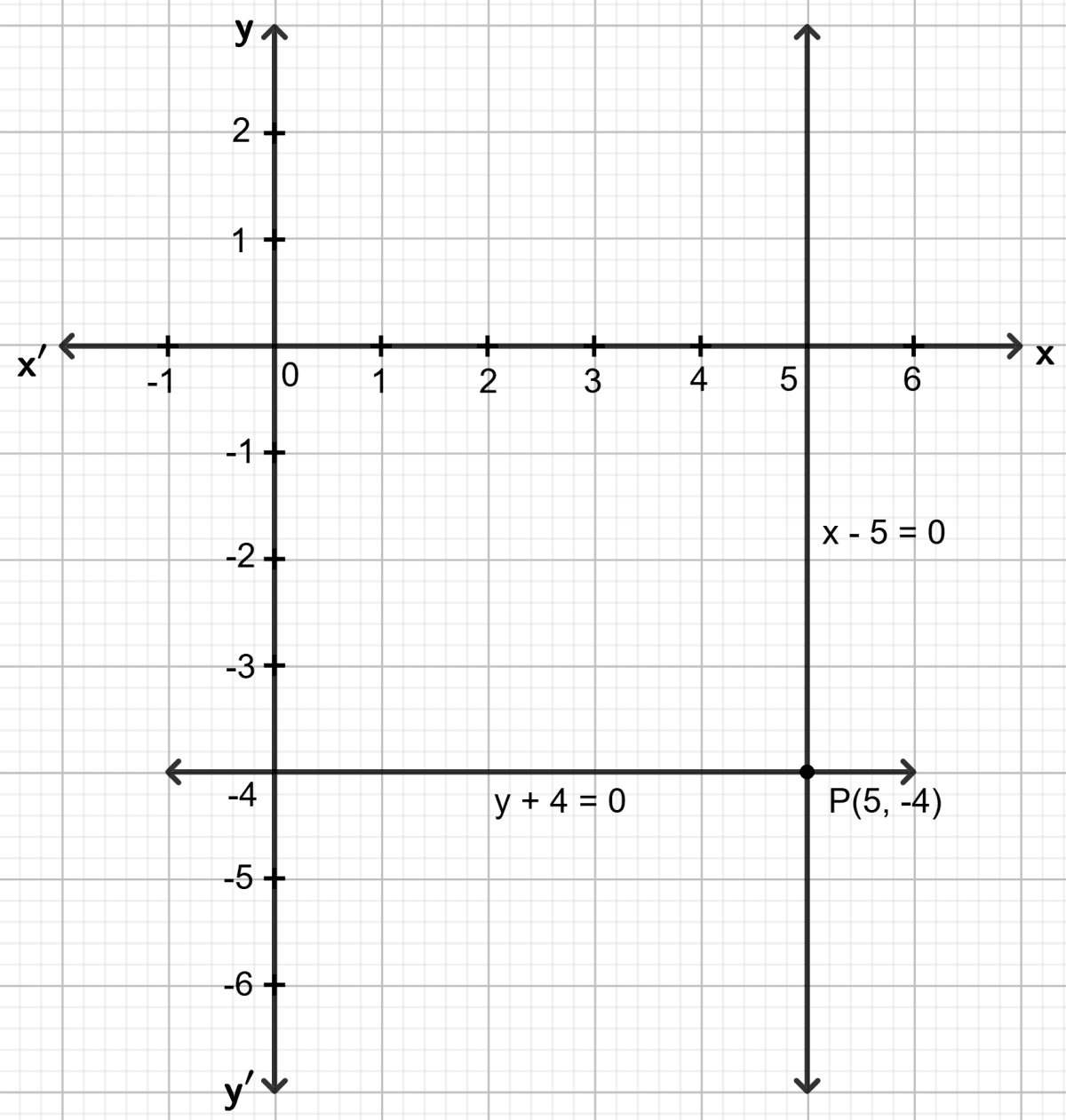
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (5, -4).
Solution of the given equations is : x = 5 and y = -4.
(ii)
First equation : 2x + y = 23
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 2, then 2 2 + y = 23 ⇒ y = 19
Let x = 4, then 2 4 + y = 23 ⇒ y = 15
Let x = 6, then 2 6 + y = 23 ⇒ y = 11
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 2 | 4 | 6 |
|---|---|---|---|
| y | 19 | 15 | 11 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation : 4x - y = 19
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 4, then 4 4 - y = 19 ⇒ y = -3
Let x = 6, then 4 6 - y = 19 ⇒ y = 5
Let x = 8, then 4 8 - y = 19 ⇒ y = 13
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 4 | 6 | 8 |
|---|---|---|---|
| y | -3 | 5 | 13 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
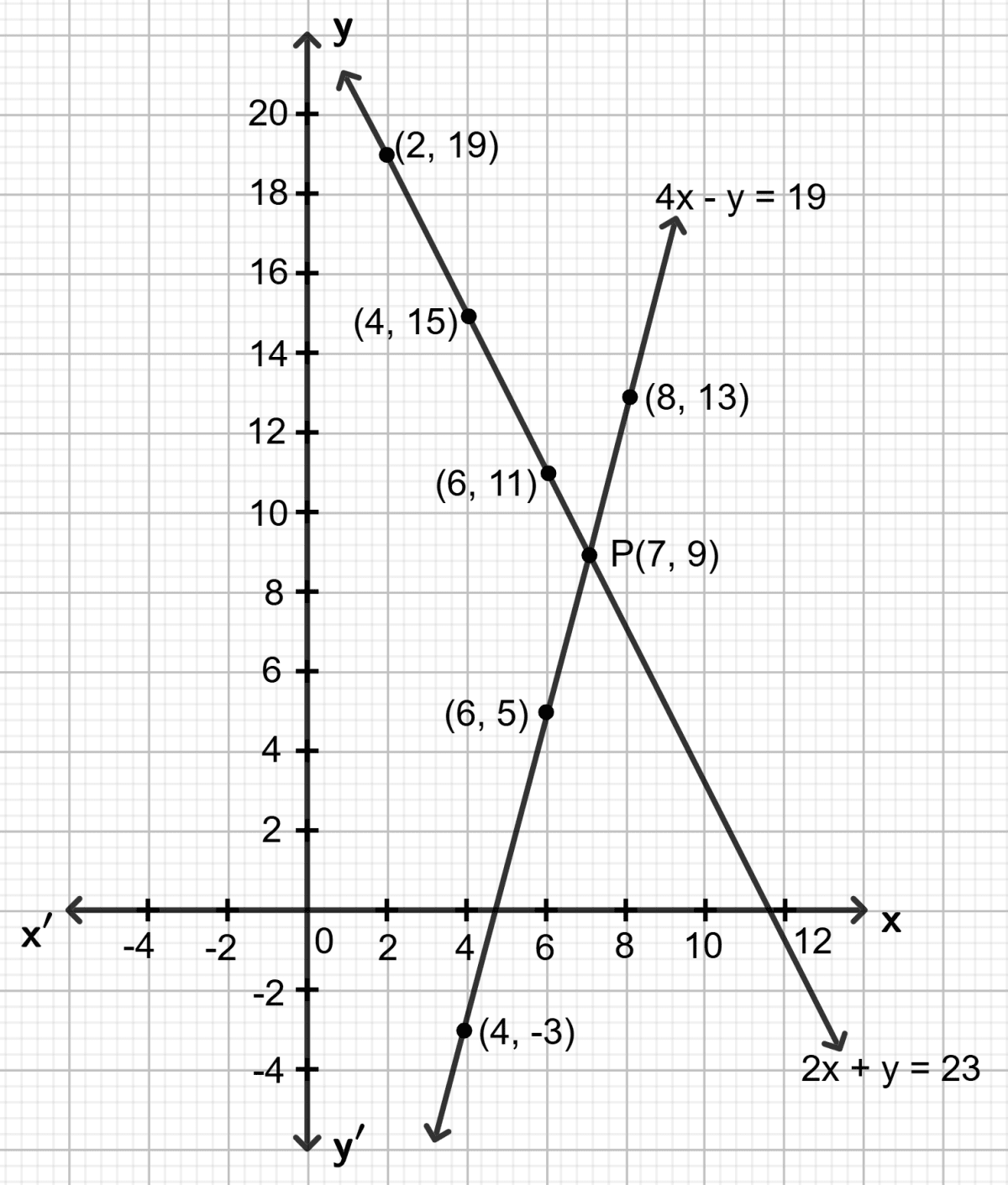
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (7, 9).
Solution of the given equations is : x = 7 and y = 9.
(iii)
First equation : 3x + 7y = 27
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 + 7y = 27 ⇒ y = 3.8
Let x = 2, then 3 2 + 7y = 27 ⇒ y = 3
Let x = 4, then 3 4 + 7y = 27 ⇒ y = 2.1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 3.8 | 3 | 2.1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then ⇒ y = 8
Let x = 1, then ⇒ y = 5.5
Let x = 2, then ⇒ y = 3
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | 8 | 5.5 | 3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
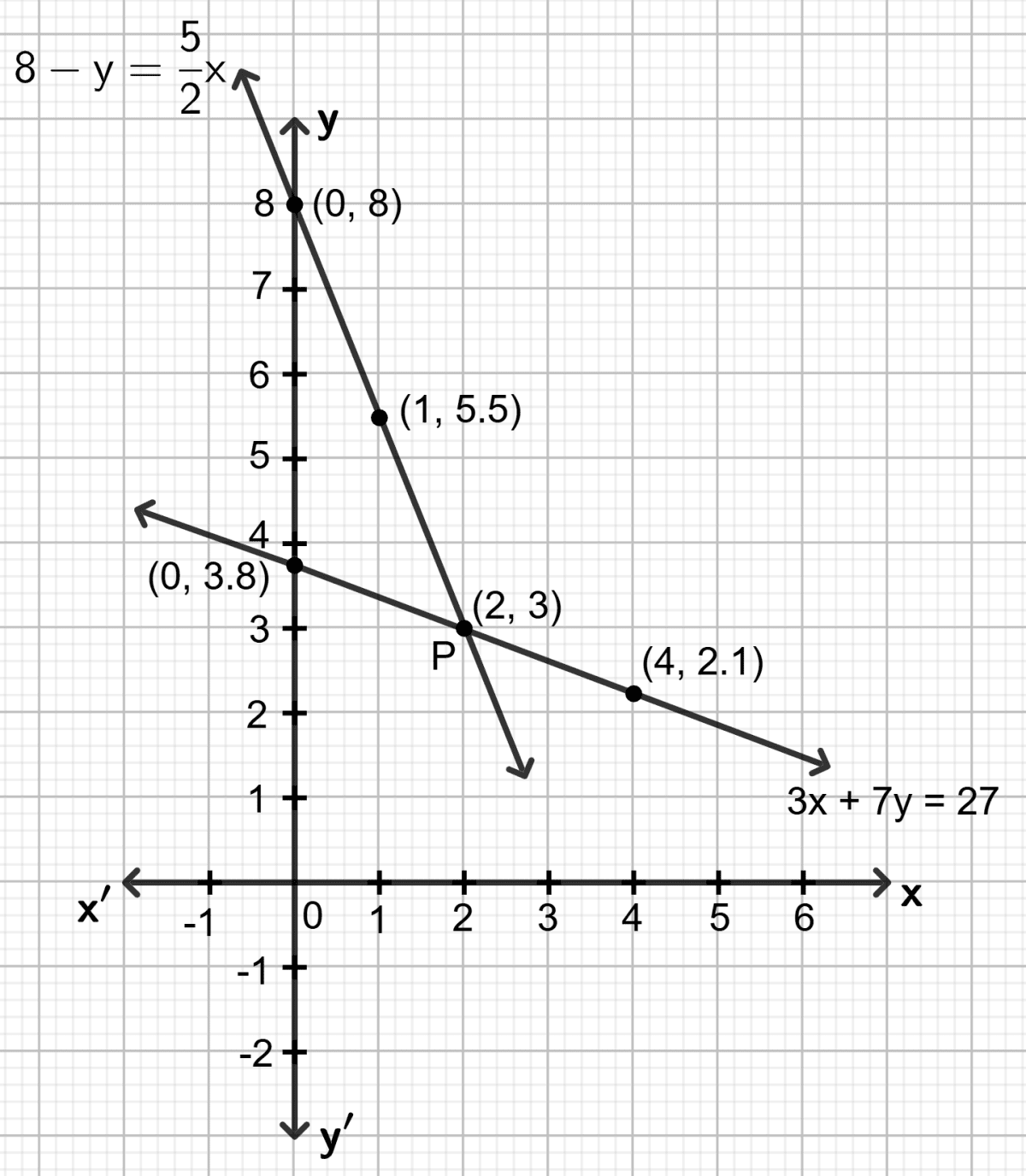
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (2, 3).
Solution of the given equations is : x = 2 and y = 3.
(iv)
First equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then ⇒ y = 0.3
Let x = 3, then ⇒ y = -0.2
Let x = 7, then ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 3 | 7 |
|---|---|---|---|
| y | 0.3 | -0.2 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then ⇒ y = -1.6
Let x = 7, then ⇒ y = -1
Let x = 14, then ⇒ y = -0.4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 7 | 14 |
|---|---|---|---|
| y | -1.6 | -1 | -0.4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
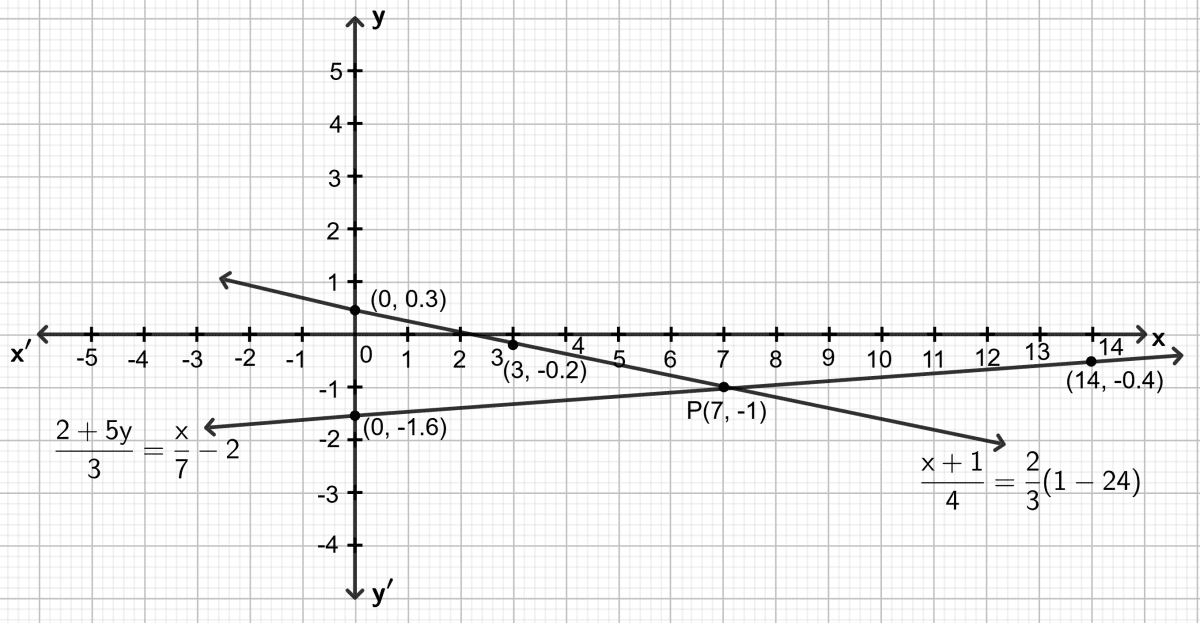
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (7, -1).
Solution of the given equations is : x = 7 and y = -1.
Answered By
7 Likes
Related Questions
The line x + 5 = 0 :
is parallel to x-axis
is parallel to y-axis
passes through (0, 0)
passes through (5, 0)
The lines y - 2 = 0 and 2x + 3y = 12 cut each other at point :
(-3, 2)
(3, -2)
(-3, -2)
(3, 2)
Solve graphically the simultaneous equations given below. Take the scale as 2 cm = 1 unit on both the axes.
x - 2y - 4 = 0
2x + y = 3Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line.
Write down the co-ordinates of the point of intersection of the two lines.