Mathematics
Solve graphically the simultaneous equations given below. Take the scale as 2 cm = 1 unit on both the axes.
x - 2y - 4 = 0
2x + y = 3
Graphical Solution
9 Likes
Answer
First equation: x - 2y - 4 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 0 - 2y - 4 = 0 ⇒ y = -2
Let x = 2, then 2 - 2y - 4 = 0 ⇒ y = -1
Let x = 4, then 4 - 2y - 4 = 0 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | -2 | -1 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 2x + y = 3
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 2 0 + y = 3 ⇒ y = 3
Let x = 2, then 2 2 + y = 3 ⇒ y = -1
Let x = 4, then 2 4 + y = 3 ⇒ y = -5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 3 | -1 | -5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
On the same graph paper, draw the graph for each given equation.
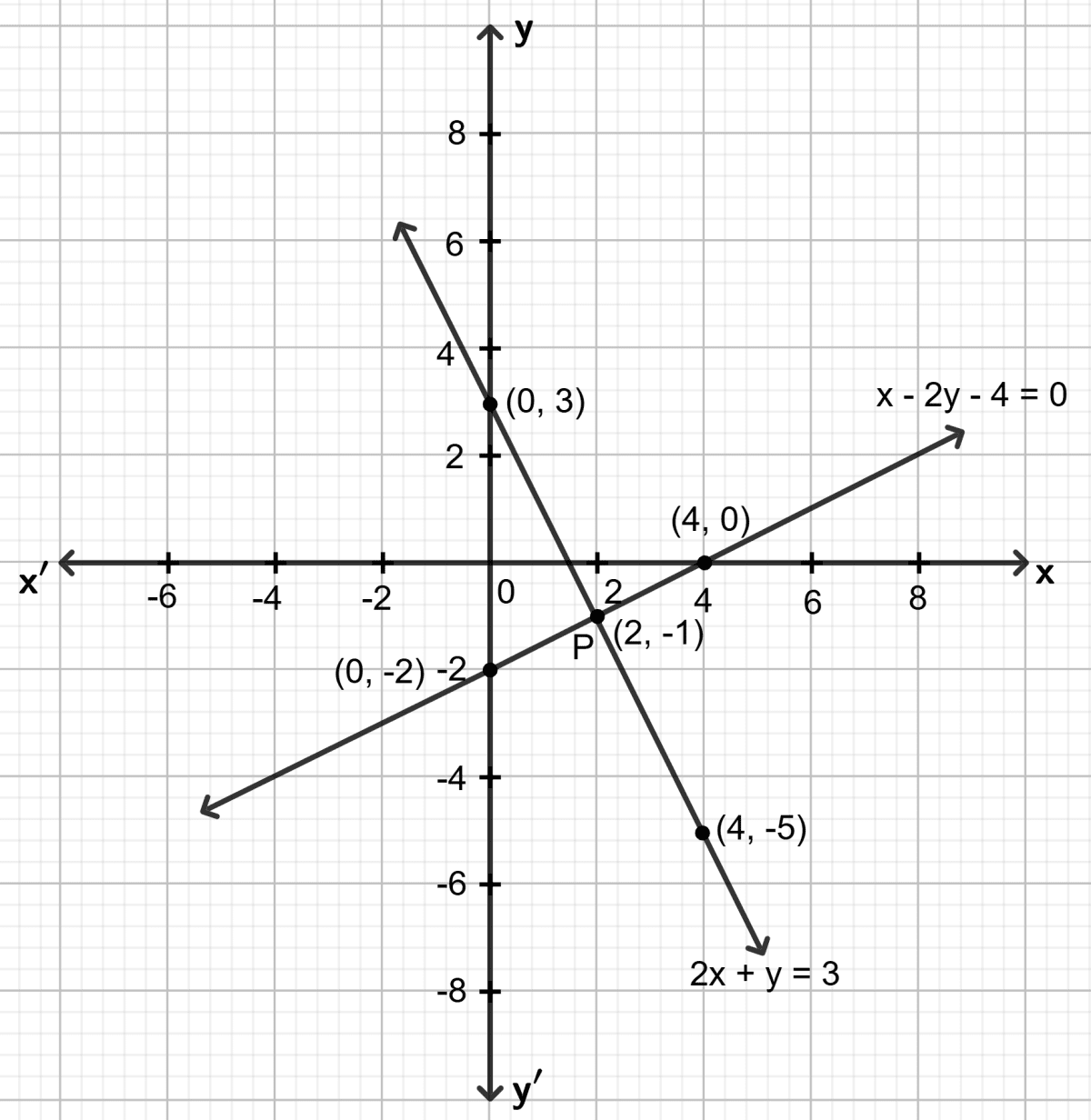
Both the straight line drawn meet the point P. As it is clear from the graph, co-ordinates of the common point P are (2, -1).
Solution of the given equation x = 2 and y = -1.
Answered By
4 Likes
Related Questions
The lines y - 2 = 0 and 2x + 3y = 12 cut each other at point :
(-3, 2)
(3, -2)
(-3, -2)
(3, 2)
Solve, graphically, the following pairs of equations :
(i)
x - 5 = 0
y + 4 = 0(ii)
2x + y = 23
4x - y = 19(iii)
3x + 7y = 27
(iv)
Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line.
Write down the co-ordinates of the point of intersection of the two lines.
Use graph paper for this question. Take 2 cm = 2 units on x-axis and 2 cm = 1 unit on y-axis.
Solve graphically the following equations :
3x + 5y = 12; 3x - 5y + 18 = 0
(Plot only three points per line)