Mathematics
Solve the following inequation and represent the solution set on the number line 2x - 5 ≤ 5x + 4 < 11, where x ∈ I.
Linear Inequations
25 Likes
Answer
Given,
2x - 5 ≤ 5x + 4 < 11
Solving L.H.S. of the equation,
⇒ 2x - 5 ≤ 5x + 4
⇒ 5x - 2x ≥ -5 - 4
⇒ 3x ≥ -9
⇒ x ≥ -3 …….(i)
Solving R.H.S. of the equation,
⇒ 5x + 4 < 11
⇒ 5x < 11 - 4
⇒ 5x < 7
⇒ x < …….(ii)
From (i) and (ii) we get,
-3 ≤ x <
Since, x ∈ I
∴ Solution set = {-3, -2, -1, 0, 1}.
Solution on the number line is :
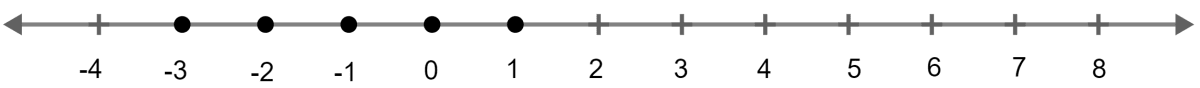
Answered By
15 Likes
Related Questions
Find the range of values of x, which satisfy :
Graph, in each of the following cases, the values of x on different real number lines:
(i) x ∈ W
(ii) x ∈ Z
(iii) x ∈ R
Given : A = {x : -8 < 5x + 2 ≤ 17, x ∈ I}
B = {x : -2 ≤ 7 + 3x < 17, x ∈ R}
Where R = {real numbers} and I = {integers}
Represent A and B on two different numbers lines. Write down elements of A ∩ B.
Given that x ∈ I, solve the inequation and graph the solution on number line :
3 ≥
The maximum value of x for the inequation 4x ≤ 12 + x is :
5
4
3
2.4