Mathematics
In square ABCD; A = (3, 4), B = (-2, 4) and C = (-2, -1). By plotting these points on a graph paper, find the co-ordinates of vertex D. Also, find the area of the square.
Coordinate Geometry
5 Likes
Answer
Plot the points A = (3, 4), B = (-2, 4) and C = (-2, -1) on the graph paper. Join point A with B and B with C.
From the graph, it is clear that the horizontal distance between the points A (3, 4) and B (-2, 4) is 5 units and the vertical distance between the points B (-2, 4) and C (-2, -1) is 5 units. Therefore, the vertical distance between the points A (3, 4) and D must be 5 units and the horizontal distance between the points C (-2, -1) and D must be 5 units.
Now, complete the square ABCD and read the coordinates of point D, as shown on the graph, D = (3, -1).
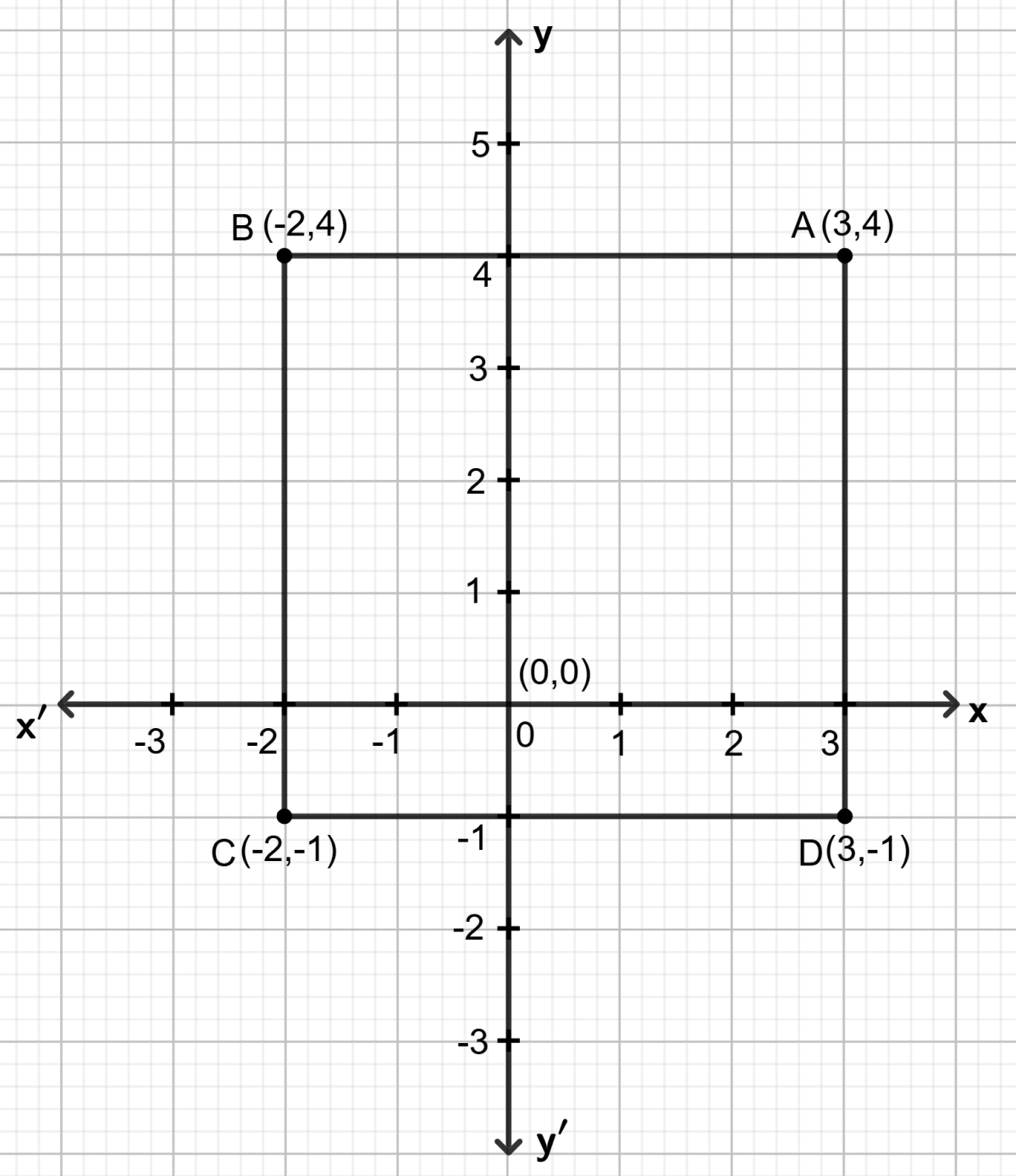
Area of the square ABCD = AD x CD
= 5 x 5 square units
= 25 square units
Hence, the coordinates of D = (3, -1) and the area of the square = 25 square units.
Answered By
4 Likes
Related Questions
By plotting the following points on the same graph paper, check whether they are collinear or not :
(-2, -1), (-1, -4) and (-4, 1)
Plot the point A (5, -7). From point A, draw AM perpendicular to x-axis and AN perpendicular to y-axis. Write the co-ordinates of points M and N.
In rectangle OABC; point O is the origin, OA = 10 units along x-axis and AB = 8 units. Find the co-ordinates of vertices A, B and C.
Draw the graph of equation x + 2y - 3 = 0. From the graph, find :
(i) x1, the value of x, when y = 3
(ii) x2, the value of x, when y = -2.