Mathematics
Statement 1: The angle between a radius and tangent of a circle is 90°.
Statement 2: At the point of contact the angle between radius and tangent is equal to one right angle.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Circles
3 Likes
Answer
A tangent line touches the circle at one point. A radius connects the center to the circumference.
The angle between a radius and tangent at the point of contact is always 90°. This is a fundamental property of circles.
So, statement 2 is true.
But, statement 1 is false as not all radius forms angle of 90° with all the tangents.
∴ Statement 1 is false, and statement 2 is true.
Hence, option 4 is the correct option.
Answered By
1 Like
Related Questions
A sector of a circle can be equal to its segment :
yes
no
none of these two
The given figure shows a circle with center O. If length of arc AQC is double of arc APB and ∠AOB = 65°; then angle AOC is :
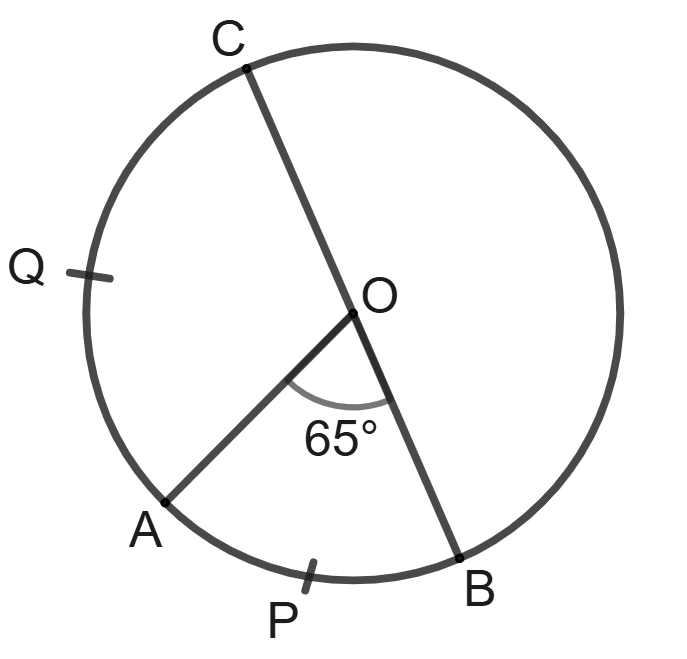
65°
2 x 65°
X 65°
none of these
Assertion (A) : The radius of a circle is 20 cm, then the length of its largest chord is also 20 cm.
Reason (R) : Longest chord of a circle is equal to its diameter.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Assertion (A) : When the radius of a circle is increased by 3 cm, its diameter will increase by 2 x 3 cm.
Reason (R) : Original radius is r cm, original diameter 2r cm
∴ Increase in length of diameter = 2(r + 3) cm - 2r
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.