Mathematics
Statement 1: At a particular time, the length of the shadow of a 50 m tower is m.
Statement 2: The sun's altitude is 30°.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Trigonometric Identities
6 Likes
Answer
In figure,
Let AB be the tower and BC be the shadow.
Join AC.
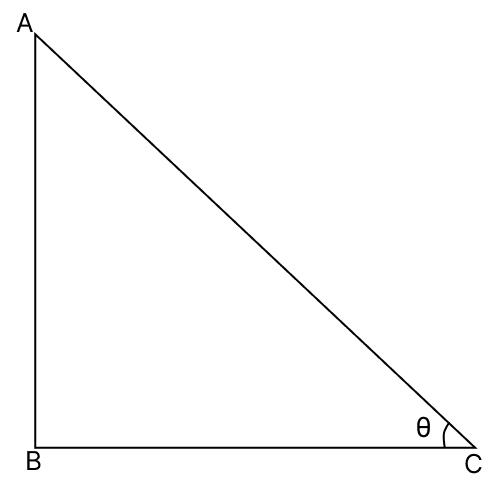
Given, AB = 50 m and BC = 50 m.
As tower is perpendicular to its shadow, thus ΔABC is a right angled triangle,
By formula,
∴ Both the statements are true.
Hence, option 1 is the correct option.
Answered By
4 Likes
Related Questions
The length of AB is:
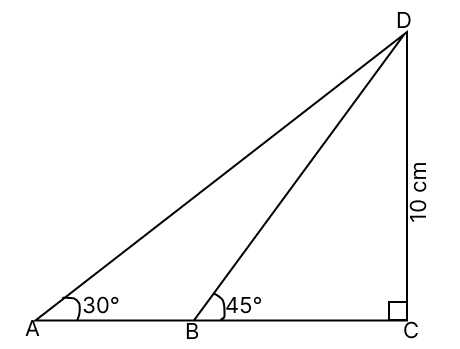
(10 - ) cm
10( - 1) cm
10 cm
10( + 1) cm
Length of AB is equal to:
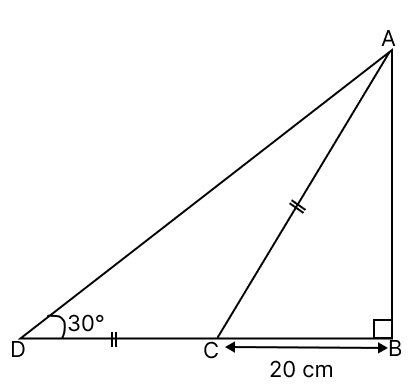
cm
cm
20 cm
none of these
Statement 1: The distance between B and C = 5 m.
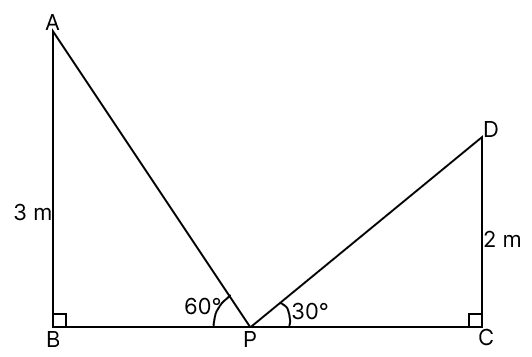
Statement 2: BC = m.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): In rhombus ABCD, angle ABC = 120° and length of its each side is 20 cm. The length of diagonal BD = 20 cm.
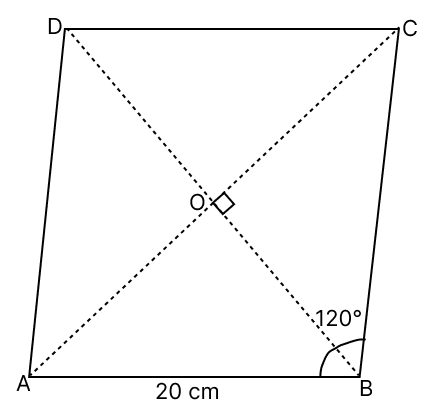
Reason (R): In ΔAOB, cos 60° = and BD = 2 x OB
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.