Mathematics
A straight line passes through the points (2, 4) and (5, -2). Taking 1 cm = 1 unit; mark these points on a graph paper and draw the straight line through these points. If points (m, -4) and (3, n) lie on the line drawn; find the values of m and n.
Graphical Solution
11 Likes
Answer
Plot the given points (2, 4) and (5, -2) on a graph paper.
Draw a straight line AB passing through these points.
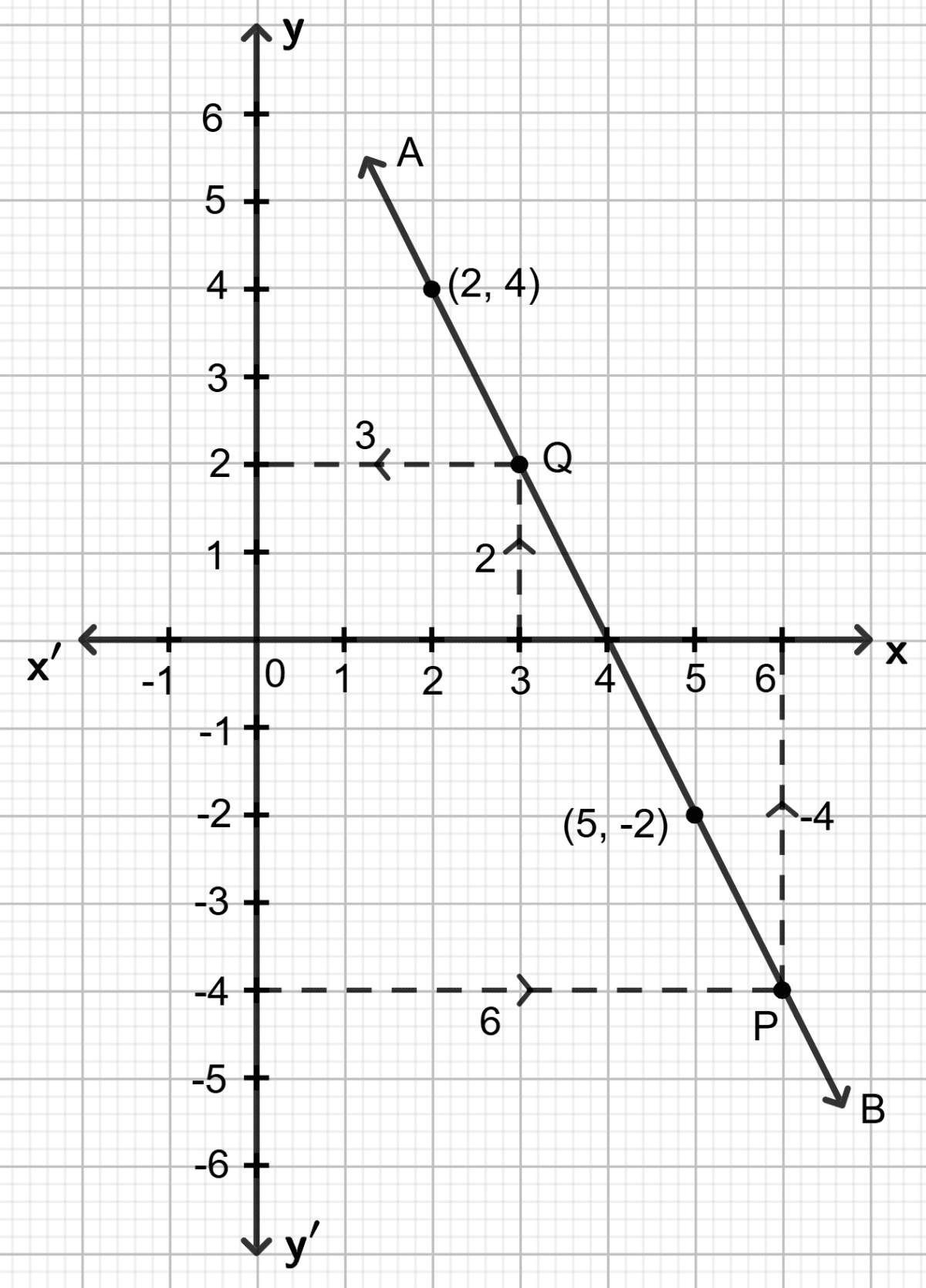
Since, point (m, -4) lies on the straight line drawn, through y = -4 draw a horizontal line which meets the straight line AB at point P. Through P, draw a vertical line which meets the x-axis at point 6.
∴ m = 6
Also, as (3, n) lies on the straight line drawn, through x = 3, draw a vertical line which meets the straight line at point Q. Through point Q, draw a horizontal line which meets the y-axis at point 2.
∴ n = 2
Hence, m = 6 and n = 2.
Answered By
6 Likes
Related Questions
Use the table given below to draw the graph.
x -5 -1 3 b 13 y -2 a 2 5 7 From your graph, find the values of 'a' and 'b'. State a linear relation between the variables x and y.
Draw the graph obtained from the table below :
x a 3 -5 5 c -1 y -1 2 b 3 4 0 Use the graph to find the values of a, b and c. State a linear relation between the variables x and y.
Draw the graph (straight line) given by equation x - 3y = 18. If the straight line drawn passes through the points (m, -5) and (6, n); find the values of m and n.
The point of intersection of lines x = 8 and y - 8 = 0 is :
(8, 8)
(8, -8)
(-8, 8)
(-8, -8)