Use the table given below to draw the graph.

x	-5	-1	3	b	13
y	-2	a	2	5	7

From your graph, find the values of 'a' and 'b'. State a linear relation between the variables x and y.

Plot the given points (-5, -2), (3, 2) and (13, 7) on a graph paper.

Draw a straight line passing through these points.

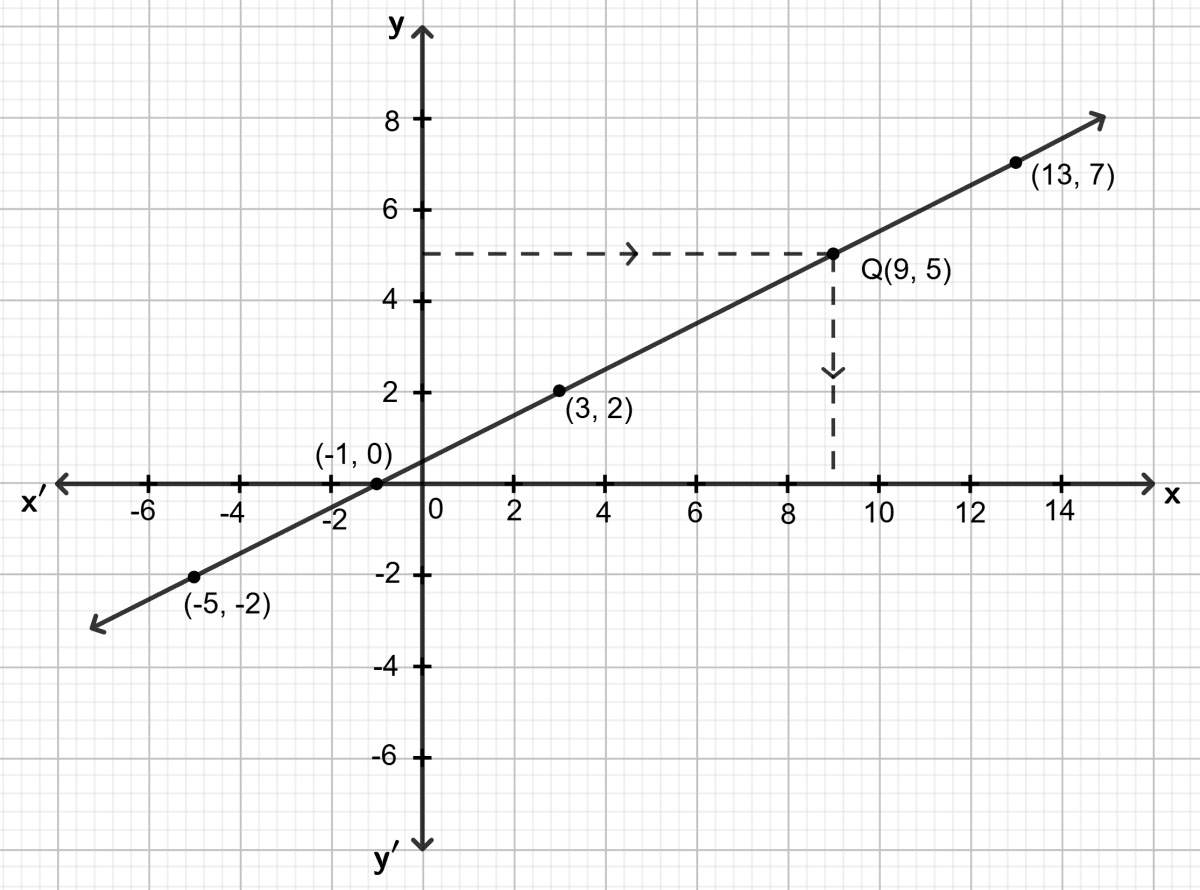
To find the value of 'a':

From the graph, y = 0 when x = −1.

∴ a = 0

To find the value of 'b':

Through y = 5, draw a horizontal line which meets the graph at a point, say Q. Through Q, draw a vertical line which meets the x-axis at x = 9.

∴ b = 9

Let the linear relation between the variable x and y be y = mx + c.

Since, the graph passes through the point (-5, -2); substitute x = -5 and y = -2 in y = mx + c.

This gives -2 = -5m + c ……………(1)

Again, the graph passes through the point (3, 2); substitute x = 3 and y = 2 in y = mx + c

This gives 2 = 3m + c ……………(2)

Subtracting (2) from (1),

-2 - 2 = -5m + c -3m - c

⇒ -4 = -8m

⇒ m = $\dfrac{4}{8}$

⇒ m = $\dfrac{1}{2}$

substituting the value of m in equation (1),

-2 = -5 $\times \dfrac{1}{2}$ + c

⇒-2 = $\dfrac{-5}{2}$ + c

⇒-2 + $\dfrac{5}{2}$ = c

⇒ $\dfrac{-4}{2} + \dfrac{5}{2}$ = c

⇒ c = $\dfrac{1}{2}$

∴ Required relation is : y = mx + c i.e. y = $\dfrac{x + 1}{2}$

Hence, a = 0 and b = 9. Linear relation : y = $\dfrac{x + 1}{2}$.