KnowledgeBoat Logo
|

Mathematics

Assertion (A) : If ∠A + ∠B = 90°, h = 16×9\sqrt{16 \times 9} cm

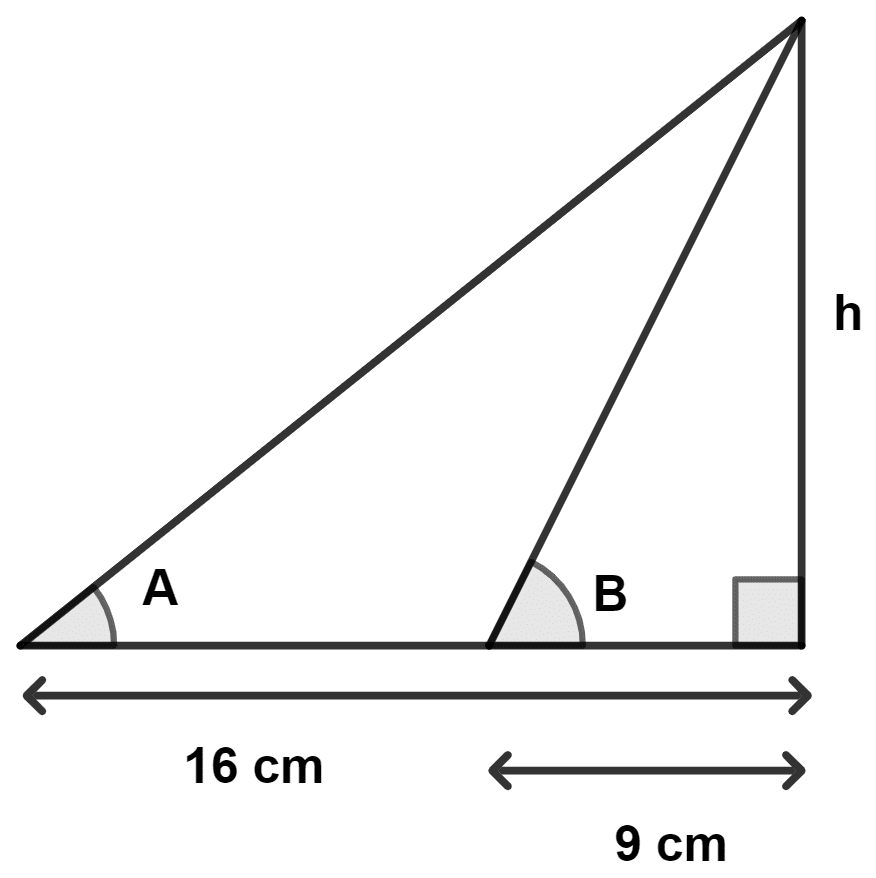
Assertion (A) : If ∠A + ∠B = 90°, h = √16 x 9 cm. Reason (R) : tan A = h/16 and tan B = h/9. Assertion-Reasoning Type Questions, Concise Mathematics Solutions ICSE Class 10.

Reason (R) : tan A = h16\dfrac{h}{16} and tan B = h9\dfrac{h}{9}. Also, A = 90° - B ⇒ tan A = cot B ⇒ tan A × tan B = 1

  1. A is true, R is false.

  2. A is false, R is true.

  3. Both A and R are true.

  4. Both A and R are false.

Trigonometric Identities

1 Like

Answer

From figure,

tan B = h9\dfrac{h}{9} ………(1)

tan A = h16\dfrac{h}{16} ………(2)

Given,

∠A + ∠B = 90°

∠A = 90° - ∠B

Substituting value of ∠A in equation (2), we get :

⇒ tan (90° - B) = h16\dfrac{h}{16}

⇒ cot B = h16\dfrac{h}{16} ……..(3)

Multiplying equation (1) and (3), we get :

⇒ tan B. cot B = h9×h16\dfrac{h}{9} \times \dfrac{h}{16}

⇒ 1 = h216×9\dfrac{h^2}{16 \times 9}

⇒ h2 = 16 × 9

⇒ h = 16×9\sqrt{16 \times 9}.

∴ Assertion (A) and Reason (R) are true.

Hence, Option 3 is the correct option.

Answered By

3 Likes

Related Questions