Mathematics
Assertion (A) : Lower quartile for the data 9, 11, 15, 19, 17, 13, 7 is 9.
Reason (R) : For finding quartiles, the given data are arranged in descending order of their magnitudes, then lower quartile (Q1) = , depending whether n is even or odd.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Statistics
2 Likes
Answer
Data : 9, 11, 15, 19, 17, 13, 7
Arranging the data in ascending order, we get :
7, 9, 11, 13, 15, 17, 19.
Since, n = 7, which is odd.
By formula,
Lower quartile =
= 2nd term = 9.
∴ Assertion (A) is true.
For finding quartiles, the given data are arranged in ascending order of their magnitudes, then lower quartile (Q1) = , depending whether n is even or odd.
∴ Reason (R) is false.
Hence, Option 1 is the correct option.
Answered By
1 Like
Related Questions
Assertion (A) : Multiplicative inverse of (sec θ - tan θ) is (sec θ + tan θ).
Reason (R) : sec2 θ - tan2 θ = 1.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : If ∠A + ∠B = 90°, h = cm
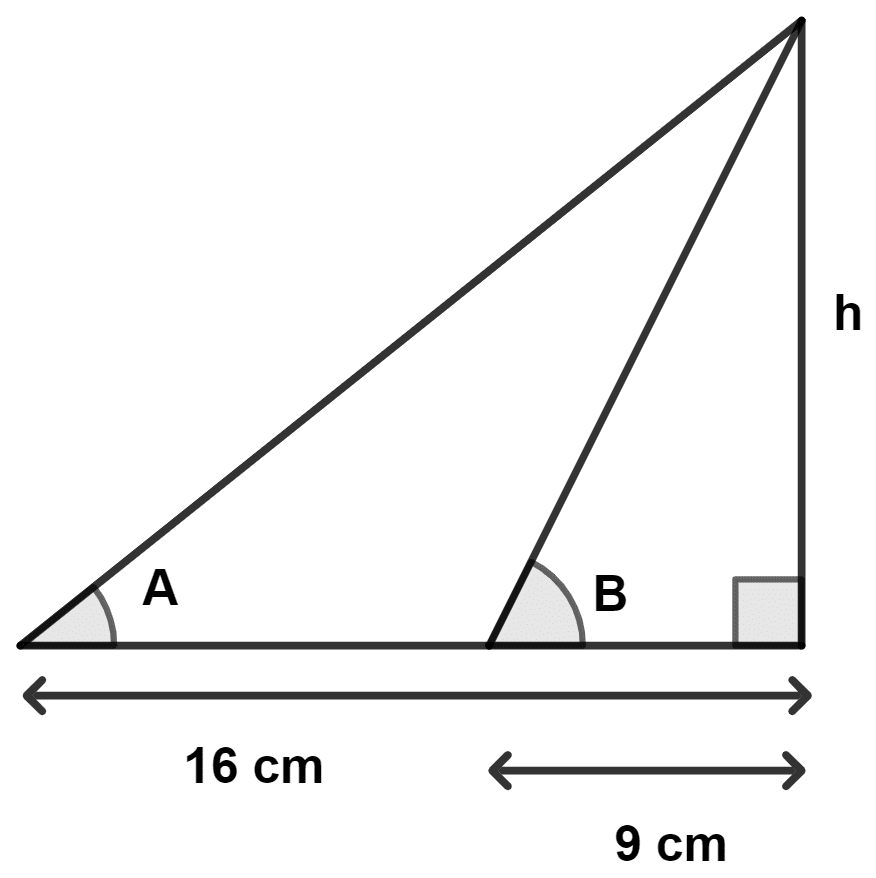
Reason (R) : tan A = and tan B = . Also, A = 90° - B ⇒ tan A = cot B ⇒ tan A × tan B = 1
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : The mean age of nine boys is 28 years. If one new boy joins them, new mean age becomes 29 years. The age of new boy is (29 - 28) × 10 years.
Reason (R) : The age of new boy is 29 × 10 - 28 × 9 years.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Assertion (A) : In tossing two dice simultaneously, n(S) = 36, where S is sample space.
Reason (R) : If a die is tossed n times or n dice are tossed simultaneously, the number of all possible outcomes = 2n.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.