Mathematics
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Mensuration
4 Likes
Answer
Given:
Sum of the areas of two squares = 400 cm2.
The difference of their perimeters = 16 cm
Let a and b be the sides of 2 square.
Sum of Areas,
⇒ a2 + b2 = 400 ……………(1)
Difference of Perimeters,
⇒ 4a - 4b = 16
⇒ 4(a - b) = 16
⇒ a - b =
⇒ a - b = 4
⇒ a = 4 + b
Substituting the value of a in equation (1), we get
⇒ (4 + b)2 + b2 = 400
⇒ 42 + b2 + 2 x 4 x b + b2 = 400
⇒ 16 + b2 + 8b + b2 = 400
⇒ 16 + 2b2 + 8b - 400 = 0
⇒ 2b2 + 8b - 384 = 0
⇒ b2 + 4b - 192 = 0
⇒ b2 + 16b - 12b - 192 = 0
⇒ b(b + 16) - 12(b + 16) = 0
⇒ (b + 16)(b - 12) = 0
⇒ b = - 16 or 12
Since the side of a square cannot be negative, b = 12 cm.
So, a = 4 + b = 16 cm
Hence, the sides of the squares are 16 cm and 12 cm.
Answered By
1 Like
Related Questions
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Using the information in the following figure, find the area of the trapezium.
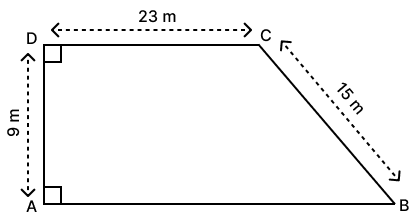
Find the area and the perimeter of a square with diagonal 24 cm.
[Take = 1.41].
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area of the circle.