The area of a rhombus is 216 sq. cm. If its one diagonal is 24 cm; find :

(i) length of its other diagonal,

(ii) length of its side,

(iii) perimeter of the rhombus.

(i) Given:

Area of rhombus = 216 sq. cm

One diagonal = 24 cm

Let d be the other diagonal of rhombus.

Area = $\dfrac{1}{2}$ x product of diagonals

⇒ 216 = $\dfrac{1}{2}$ x 24 x d

⇒ 216 = 12 x d

⇒ d = $\dfrac{216}{12}$

⇒ d = 18

Hence, the length of other diagonal is 18 cm.

(ii) The rhombus is shown in the figure below:

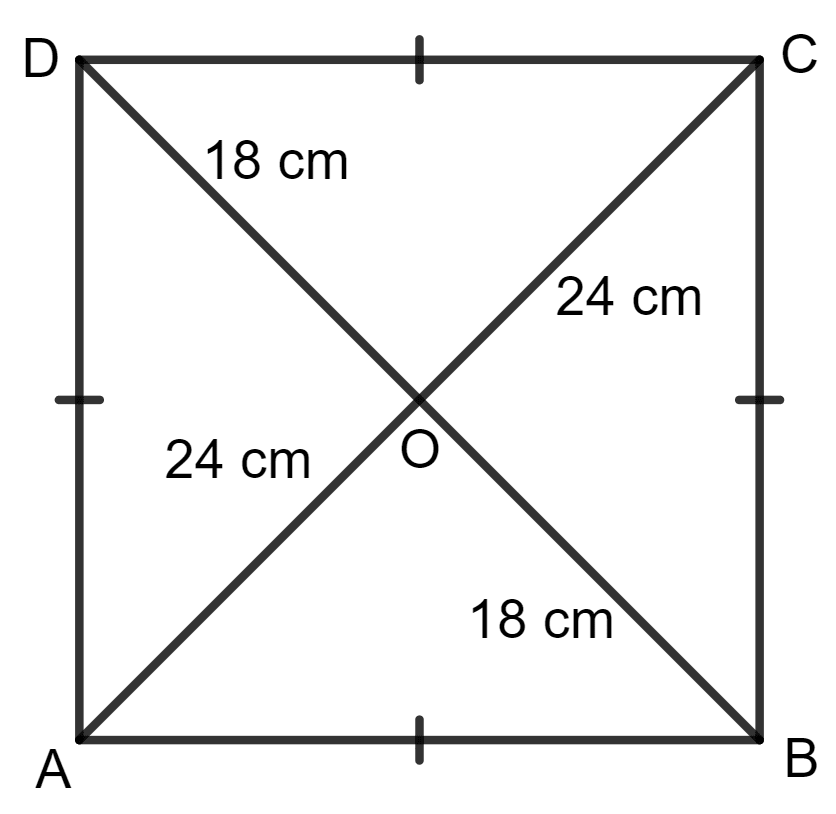
Diagonal AC = 24 cm

Then, OA = OC = $\dfrac{24}{2}$ = 12 cm

Diagonal BD = 18 cm

Then, OB = OD = $\dfrac{18}{2}$ = 9 cm

Since the diagonals of a rhombus bisect at 90°.

Applying pythagoras theorem in Δ AOB, we get:

AB² = OA² + OB²

⇒ AB² = (12)² + (9)²

⇒ AB² = 144 + 81

⇒ AB² = 225

⇒ AB = $\sqrt{225}$

⇒ AB = 15 cm

Hence, the length of each side of the rhombus is 15 cm.

(iii) Perimeter of the rhombus = 4 x side

= 4 x 15 cm

= 60 cm

Hence, the perimeter of the rhombus 60 cm.