Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.

By joining diagonal BD, the parallelogram is divided into two triangles. Let the sides of Δ ABD be:

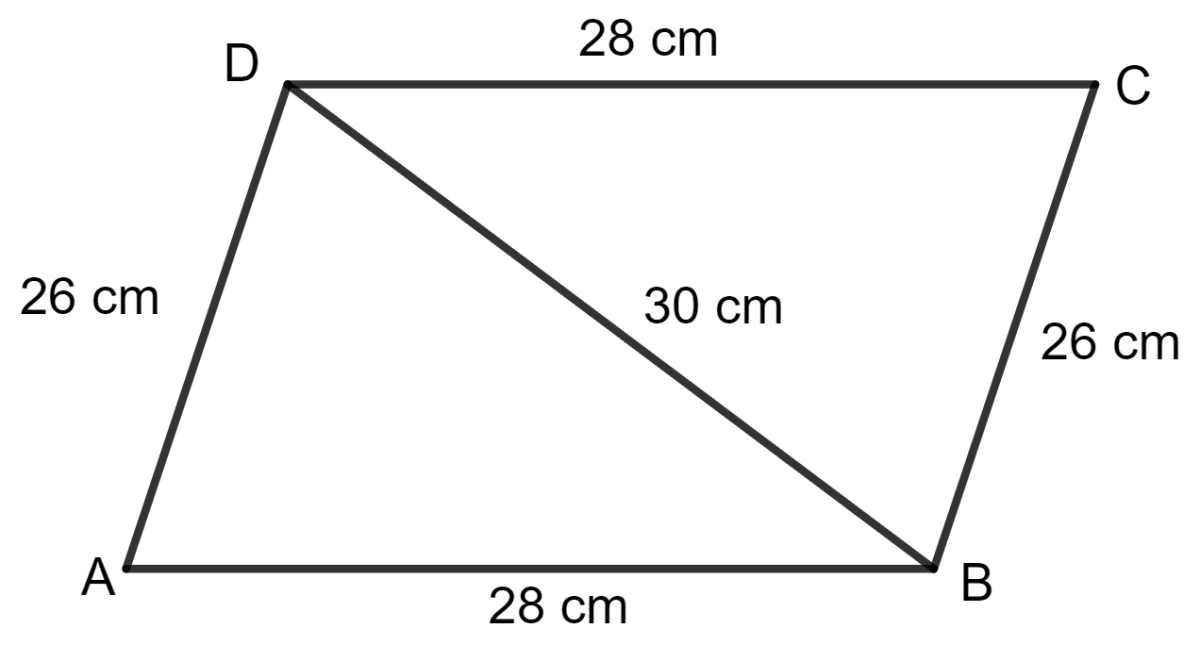
a = 28 cm, b = 26 cm and c = 30 cm.

The semi-perimeter s:

$∵ s = \dfrac{a + b + c}{2}\\[1em] = \dfrac{28 + 26 + 30}{2}\\[1em] = \dfrac{84}{2}\\[1em] = 42$

∵ Area of triangle = $\sqrt{s(s - a)(s - b)(s - c)}$

= $\sqrt{42(42 - 28)(42 - 26)(42 - 30)}$ cm²

= $\sqrt{42 \times 14 \times 16 \times 12}$ cm²

= $\sqrt{112,896}$ cm²

= 336 cm²

Area of parallelogram ABCD = 2 x area of Δ ABD

= 2 x 336 cm²

= 672 cm²

Let h be the distance between the shorter sides.

Area of the parallelogram = base x height

⇒ 26 x h = 672

⇒ h = $\dfrac{672}{26}$

⇒ h = 25.84 cm

Hence, the area of the parallelogram is 672 cm² and the distance between the shorter sides is 25.84 cm.