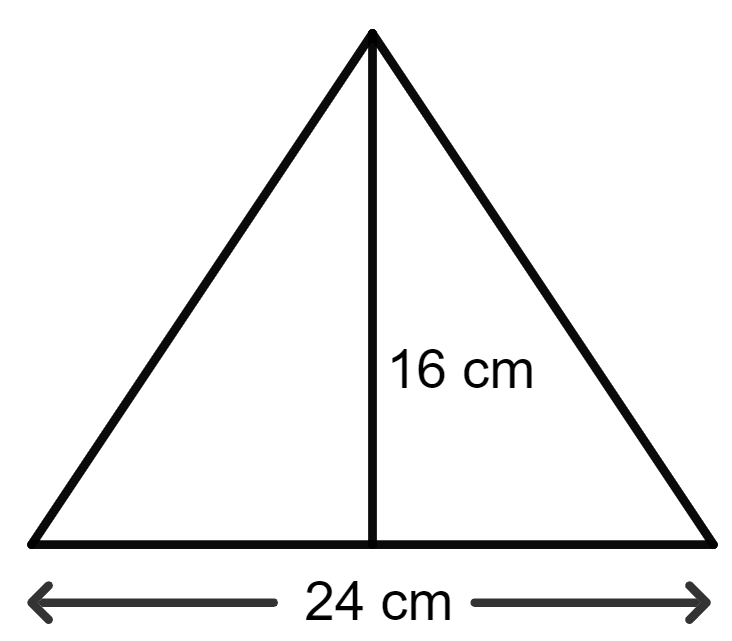
The area of a rhombus is equal to the area of a triangle. If base of triangle is 24 cm, its corresponding altitude is 16 cm and one of the diagonals of the rhombus is 19.2 cm, find its other diagonal.

Given:

The area of a rhombus = The area of a triangle

The base of the triangle = 24 cm

The altitude of the triangle = 16 cm

One of the diagonals of the rhombus = 19.2 cm

As we know, the area of a triangle = $\dfrac{1}{2}$ x base x altitude

= $\dfrac{1}{2}$ x 24 x 16 cm²

= $\dfrac{1}{2}$ x 384 cm²

= 192 cm²

Let the length of the other diagonal of the rhombus be d.

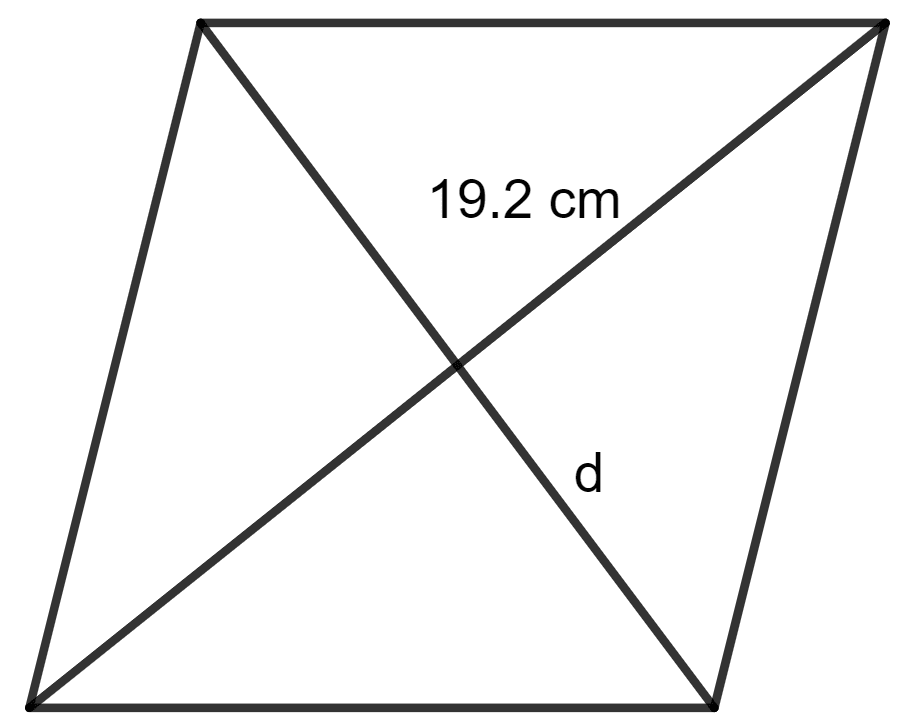
The area of the rhombus = $\dfrac{1}{2}$ x (product of diagonals)

⇒ $\dfrac{1}{2}$ x (19.2 x d) = 192

⇒ 9.6 x d = 192

⇒ d = $\dfrac{192}{9.6}$

⇒ d = 20 cm

Hence, the length of the other diagonal is 20 cm.