The area of a trapezium is 279 sq. cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.

Given:

The area of a trapezium = 279 sq. cm

The distance between its two parallel sides = 18 cm.

One of the parallel sides is longer than the other side by 5 cm.

Let one of the parallel sides be a. Then, the other parallel side is a - 5.

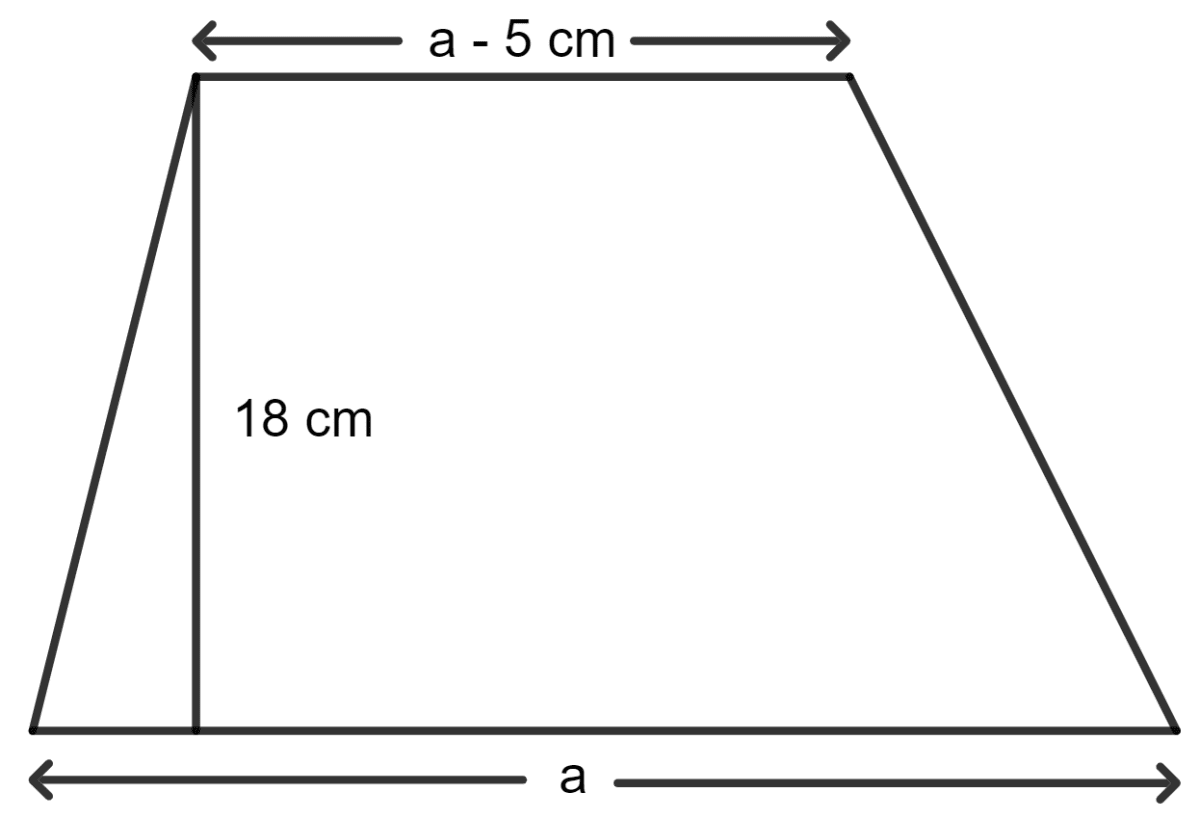
As we know, the area of a trapezium = $\dfrac{1}{2}$ (sum of parallel sides) x distance between the parallel sides

Substituting the given values:

⇒ 279 = $\dfrac{1}{2}$ (a + a - 5) x 18

⇒ 279 = $\dfrac{1}{2}$ (2a - 5) x 18

⇒ 279 = $\dfrac{1}{2}$ (36a - 90)

⇒ 279 = 18a - 45

⇒ 18a = 279 + 45

⇒ 18a = 324

⇒ a = $\dfrac{324}{18}$

⇒ a = 18 cm

So, the parallel sides are 18 cm and (18 - 5) = 13 cm.

Hence, the lengths of the parallel sides are 18 cm and 13 cm, respectively.