KnowledgeBoat Logo
|

Mathematics

The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.

Mensuration

11 Likes

Answer

Given:

Diagonal of the rectangular plot = 34 m

Perimeter of the rectangular plot = 92 m

Let l be the length and b be the breadth of the rectangular plot.

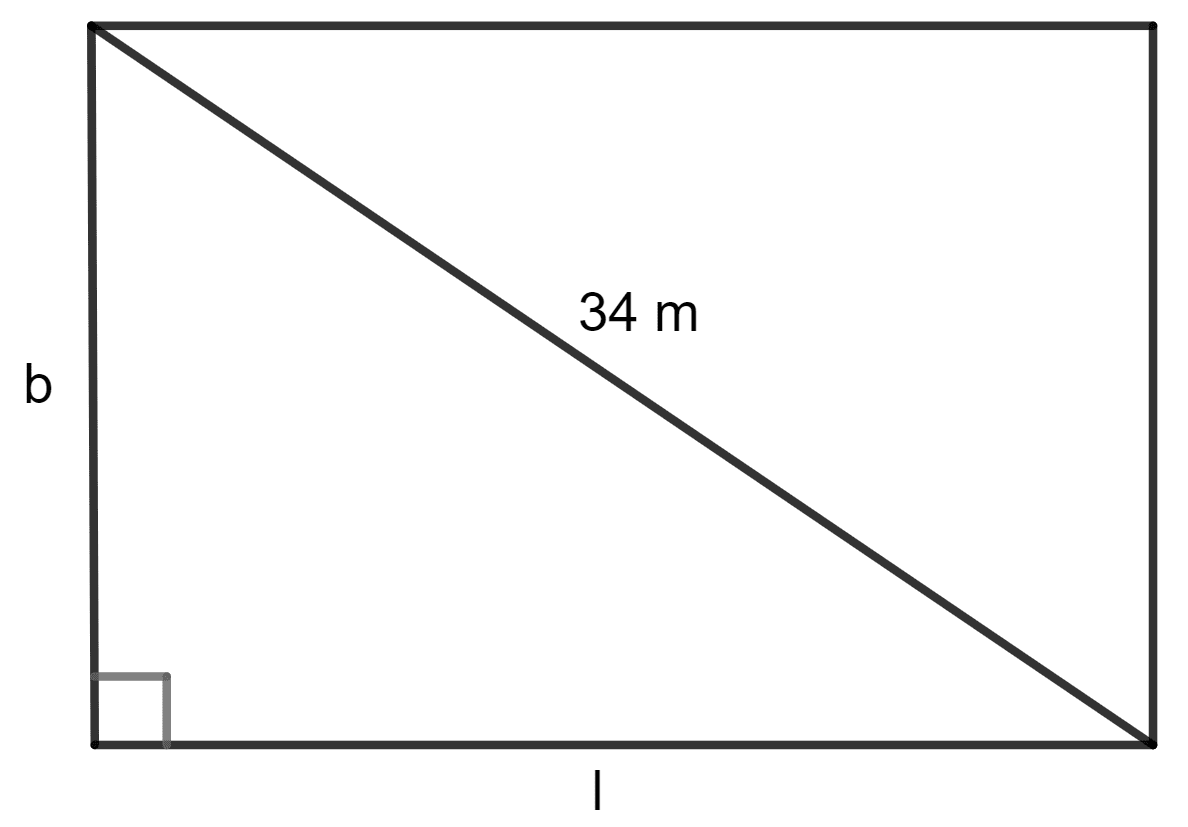
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area. Area and Perimeter of Plane Figures, Concise Mathematics Solutions ICSE Class 9.

Perimeter = 2(l + b)

⇒ 2(l + b) = 92

⇒ l + b = 922\dfrac{92}{2}

⇒ l + b = 46

Squaring both side,

⇒ (l + b)2 = 462

⇒ l2 + b2 + 2lb = 2,116 ……………(1)

As all the angles of rectangle are 90°, we can use the Pythagoras theorem,

Base2 + Height2 = Hypotenuse2

⇒ l2 + b2 = 342

⇒ l2 + b2 = 1,156

Using equation (1), we get

⇒ 2,116 - 2lb = 1,156

⇒ 2,116 - 1,156 = 2lb

⇒ 960 = 2lb

⇒ lb = 9602\dfrac{960}{2}

⇒ lb = 480

Hence, the area of the rectangular plot is 480 m2.

Answered By

5 Likes

Related Questions