Mathematics
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centres is 10 cm. Find the radii of the two circles.
Mensuration
9 Likes
Answer
Let r1 and r2 be the radii of the two circles.
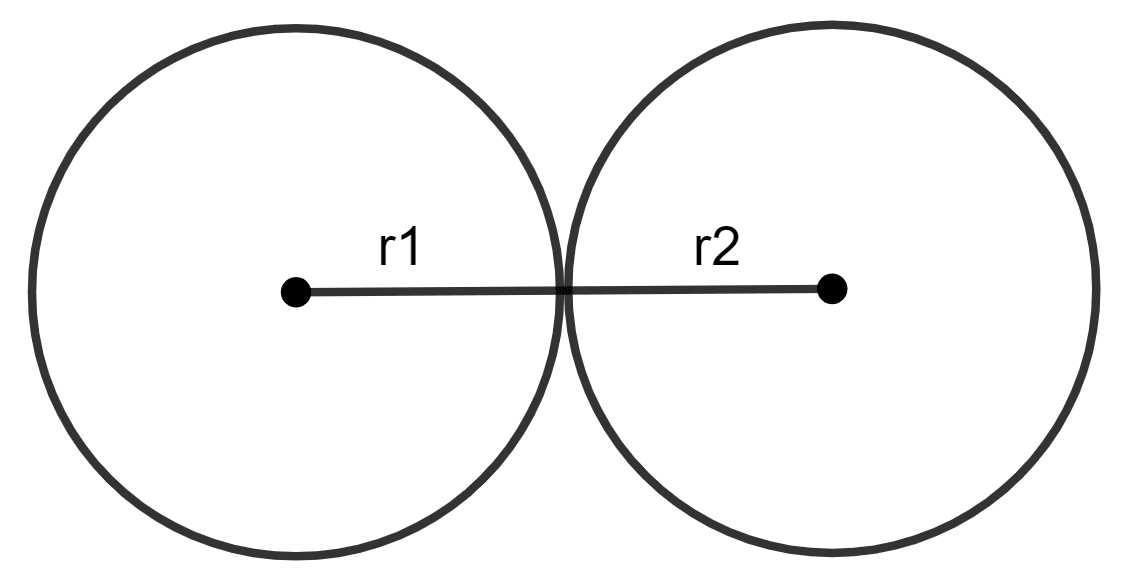
Sum of the areas = 58π
⇒ A1 + A2 = 58π
⇒ πr12 + πr22 = 58π
⇒ π(r12 + r22) = 58π
⇒ (r12 + r22) = 58
⇒ r12 + r22 = 58 ……………(1)
Also, since the circles touch externally, the sum of their radii equals the distance between their centers.
r1 + r2 = 10
⇒ r1 = 10 - r2
Substituting the value of r1 in equation (1),
⇒ (10 - r2)2 + r22 = 58
⇒ 102 + r22 - 2 x 10 x r2 + r22 = 58
⇒ 100 + 2r22 - 20r2 = 58
⇒ 100 + 2r22 - 20r2 - 58 = 0
⇒ 2r22 - 20r2 - 42 = 0
⇒ r22 - 10r2 - 21 = 0
⇒ r22 - 3r2 - 7r2 - 21 = 0
⇒ r2(r2 - 3) - 7(r2 - 3) = 0
⇒ (r2 - 3)(r2 - 7) = 0
⇒ r2 = 3 cm or 7 cm
Using equation (1), we find r1:
If r2 = 3, then r1 = 10 - 3 = 7 cm
If r2 = 7, then r1 = 10 - 7 = 3 cm
Hence, the radii of the two circles are 7 cm and 3 cm.
Answered By
6 Likes
Related Questions
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
The cost of fencing a circular field at the rate of ₹ 240 per metre is ₹ 52,800. The field is to be ploughed at the rate of ₹ 12.50 per m2. Find the cost of ploughing the field.
The given figure shows a rectangle ABCD inscribed in a circle as shown alongside.
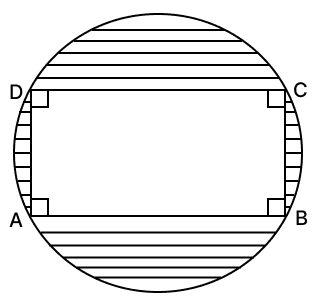
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.
A square is inscribed in a circle of radius 7 cm. Find the area of the square.