The diagonals of a quadrilateral ABCD are perpendicular to each other. Prove that the quadrilateral obtained by joining the mid-points of its adjacent sides is a rectangle.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Let ABCD be a quadrilateral where P, Q, R and S are the mid-point of AB, BC, CD and DA.

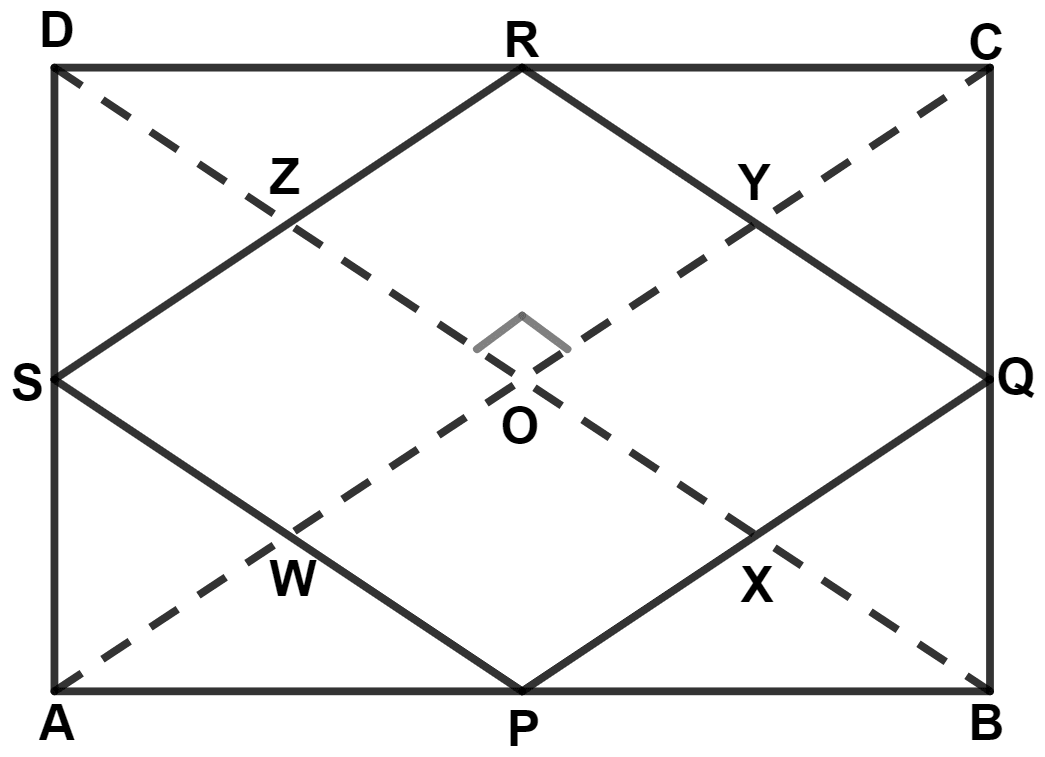
In △ ABC,

P and Q are mid-points of AB and BC respectively.

⇒ PQ = $\dfrac{1}{2}AC$ and PQ || AC. [By mid-point theorem] …….(1)

In △ ADC,

S and R are mid-points of AD and CD respectively.

⇒ SR = $\dfrac{1}{2}AC$ and SR || AC. [By mid-point theorem] …….(2)

From (1) and (2), we get :

PQ = SR and PQ || SR.

In △ BCD,

R and Q are mid-points of CD and BC respectively.

⇒ QR = $\dfrac{1}{2}BD$ and QR || BD. [By mid-point theorem] …….(3)

In △ ABD,

S and P are mid-points of AD and AB respectively.

⇒ PS = $\dfrac{1}{2}BD$ and PS || BD. [By mid-point theorem] …….(4)

From (3) and (4), we get :

QR = PS and QR || PS.

Since, diagonals of quadrilateral intersect at right angle.

∴ ∠AOD = ∠COD = AOB = ∠BOC = 90°.

From figure,

PQ || AC

∴ ∠PXO = ∠AOD = 90° (Corresponding angles are equal)

∴ ∠QXO = ∠COD = 90° (Corresponding angles are equal)

SR || AC

∴ ∠SZO = ∠AOB = 90° (Corresponding angles are equal)

∴ ∠RZO = ∠BOC = 90° (Corresponding angles are equal)

PS || BD

∴ ∠S = ∠RZO = 90° (Corresponding angles are equal)

∴ ∠P = ∠QXO = 90° (Corresponding angles are equal)

QR || BD

∴ ∠R = ∠SZO = 90° (Corresponding angles are equal)

∴ ∠Q = ∠PXO = 90° (Corresponding angles are equal)

Since, in quadrilateral PQRS,

Each interior angle is equal to 90° and opposite sides are parallel and equal.

∴ PQRS is a rectangle.

Hence, proved that the the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.