Mathematics
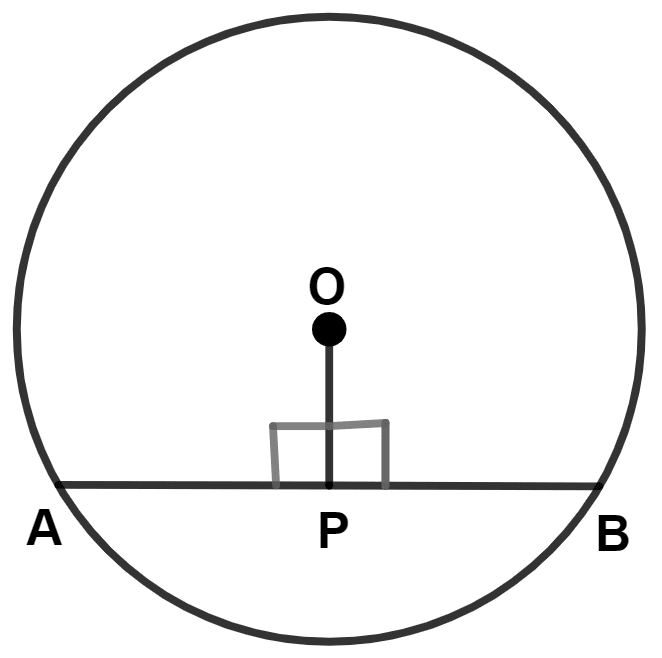
The following figure shows a circle with center O. If OP is perpendicular to AB, prove that AP = BP.
Triangles
55 Likes
Answer
Join OA and OB.
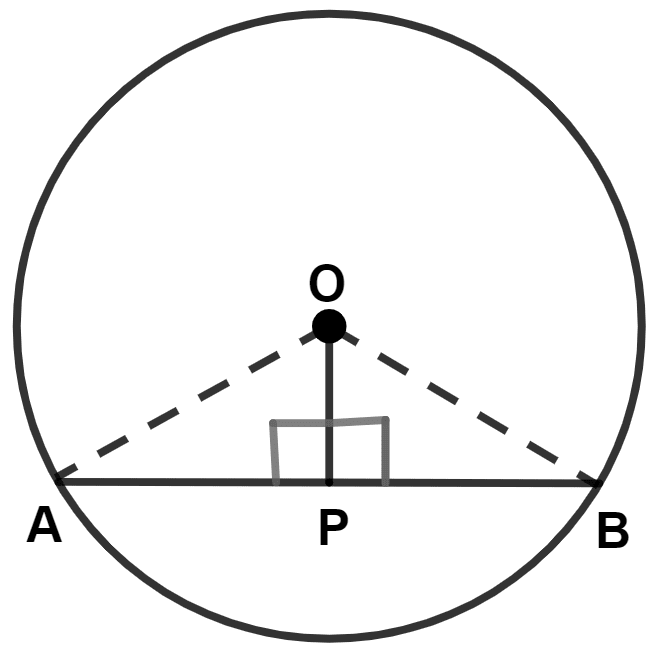
In △ OAP and △ OBP,
⇒ OP = OP (Common side)
⇒ OA = OB (Radius of same circle)
⇒ ∠OPA = ∠OPB (Both equal to 90°)
∴ △ OAP ≅ △ OBP (By R.H.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ AP = BP.
Hence, proved that AP = BP.
Answered By
36 Likes
Related Questions
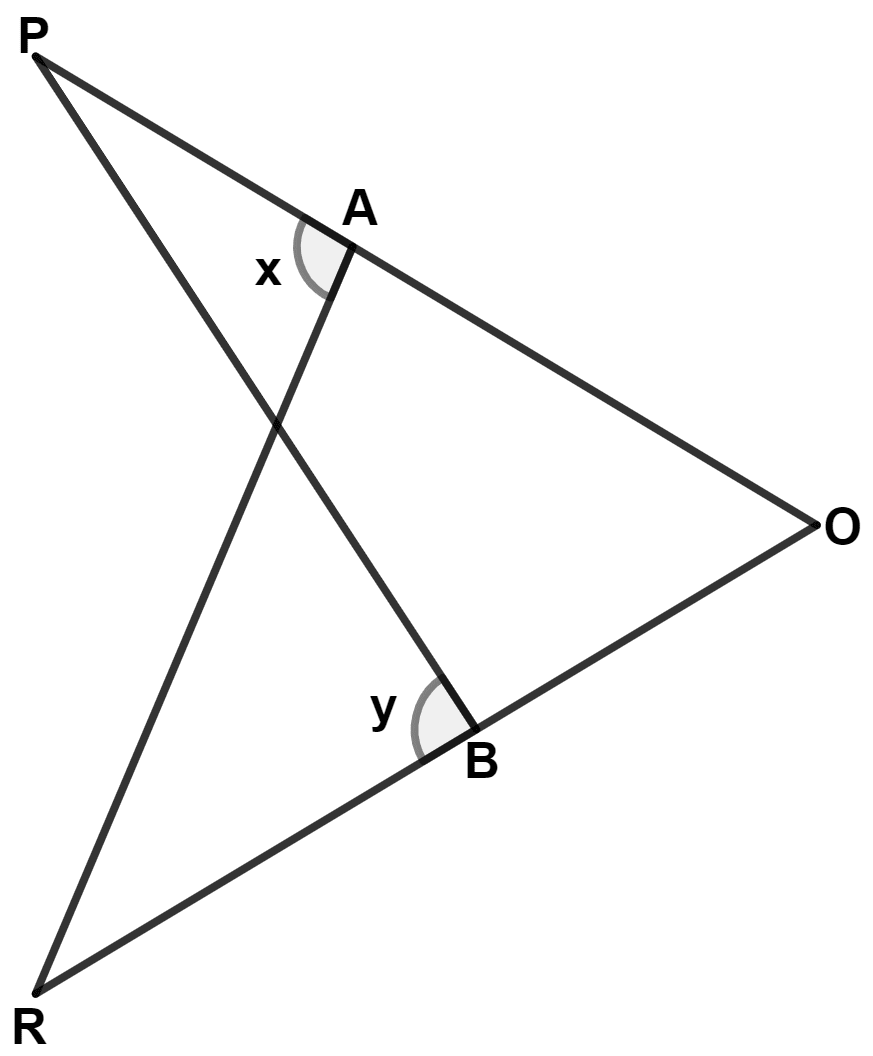
In the given figure, ∠x = ∠y and PO = RO, then :
RB = AO
BO = PA
BP = AR
RB = OB
In the given figure, BC // DA and BC = DA, then :
AB and CD bisect each other
AB ≠ CD
OA = OC
OA = OD
In a triangle ABC, D is mid-point of BC; AD is produced upto E, so that DE = AD. Prove that :
(i) △ ABD and △ ECD are congruent.
(ii) AB = EC
(iii) AB is parallel to EC.
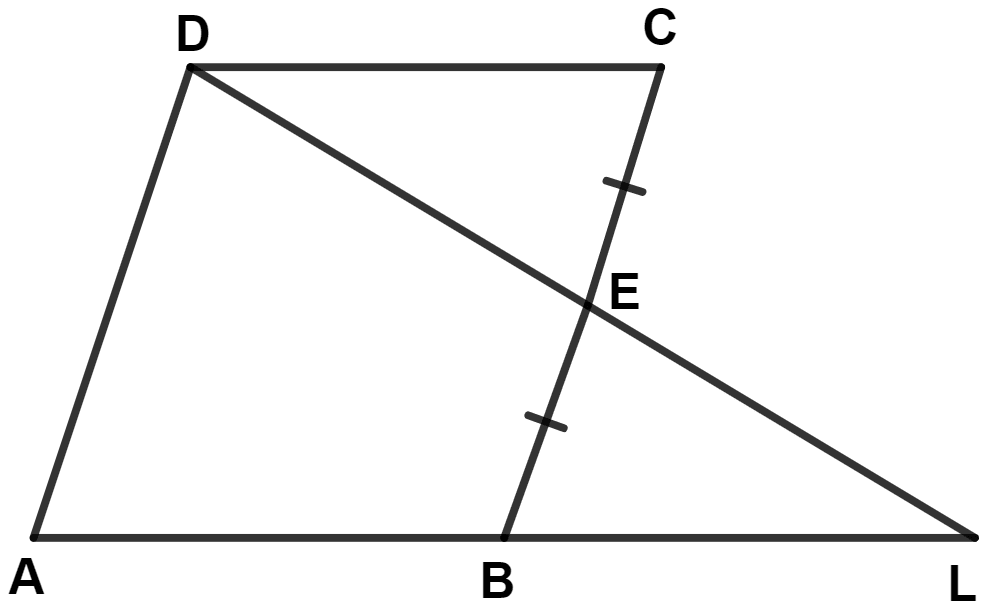
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid point of BC.
Prove that :
(i) △ DCE ≅ △ LBE
(ii) AB = BL
(iii) AL = 2DC