Mathematics
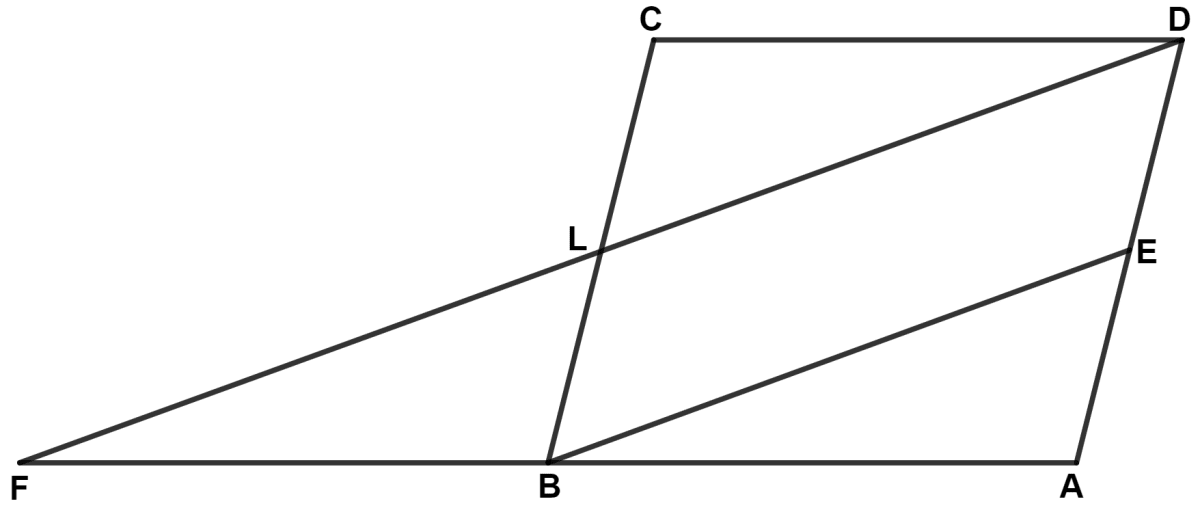
The given figure shows a parallelogram ABCD in which E is mid-point of AD and DL // EB. Then, BF is equal to :
AD
BE
AE
AB
Answer
By equal intercept theorem,
If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.
In parallelogram ABCD,
DL || EB
Since, E is mid-point of AD.
∴ AE = ED
∴ BL = LC (By equal intercept theorem)
In △ BLF and △ DLC,
⇒ ∠BLF = ∠DLC (Vertically opposite angles are equal)
⇒ BL = LC (Proved above)
⇒ ∠LBF = ∠LCD (Alternate angles are equal)
∴ △ BLF ≅ △ DLC (By A.S.A. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
∴ BF = CD ………(1)
We know that,
Opposite sides of parallelogram are equal.
∴ AB = CD ………(2)
From equation (1) and (2), we get :
⇒ BF = AB.
Hence, Option 4 is the correct option.